범위 : 5.1 나이브베이즈 ~ 5.3.2 로지스틱 회귀와 GLM

5.1 나이브베이즈
용어정리
- 조건부확률 : 여떤 사건(Y=i)이 주어졌을 때, 해당 사건 (X=i)을 관찰할 확률 P(X | Y)
- 사후확률 : 예측 정보를 통합한 후 결과의 확률 (사전확률에서는 예측변수에 대한 정보를 고려하지 않는다)
- 나이브베이즈 : 주어진 결과에 대해 예측변숫값을 관찰할 확률을 사용하여, 예측변수가 주어졌을때 결과를 관찰할 확률을 사용하다 (주로 범주형)
예측변수의 값이 동일한 모든 레코드를 찾는다
해당 레코드들이 가장 많이 속한 클래스를 정한다
새 레코드에 해당 클레스를 지정한다
베이즈 정리 : 새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신해가는 방법
나이브 베이지 : 사전확률에 추가정보의 확률을 곱해주는 것
예) 성별이 여성일 확률(사전확률) X 키가 170이상일 확율(P(x >170 | 여성) X 몸무게가 60이상일 확율(P(x >60 | 여성)
주요개념
- 나이브 베이즈는 예측변수와 결과변수 모두 범주형 이어야 한다
- 각 출력 카테고리 안에서, 어떤 예측변수의 카테고리가 가장 가능성이 높은가?를 알고자한다
- 이 정보는 주어진 예측변수 값에 대해, 결국 카테고리의 확률을 추정하는 것으로 바뀐다
5.2 판별분석
용어정리
- 공분산(covariance) : 하나의 변수가 다른 변수와 함께 변화하는 정도(유사한 크기와 방향)을 측정하는 지표
- 판별함수(discriminant function) : 예측변수에 적용했을 때, 클래스 구분을 최대화 하는 함수
- 판별 가중치 : 판별함수를 적용하여 얻은 점수를 말하며, 어떤 클래스에 속할 확률을 추정하는데 사용
2.1 공분산행렬
공분산 : 두 변수 x와 z사이의 관계를 의미하는 지료
 |
 |
- 범위 : -∞에서 +∞ (단위에 민감)
- 양수 : 두 변수는 같은 방향으로 움직이는 경향이 있음
- 음수 : 두 변수는 반대 방향으로 움직이는 경향이 있음
- 0 : 두 변수의 상관관계가 없음, 독립적인 관계
* 상관관계 : 두 변수 간의 관계의 강도와 방향을 나타내는 무단위 척도
 |
 |
- 공분산을 두 변수의 표준편차로 나눈 값으로, 두 변수의 분포에 관계없이 비교가능
2.2 피셔의 선형판별 ( LDA : Linear Discriminant Analysis)
LAD : 데이터 분포를 학습해 결정경계를 만들어 데이터를 분류하는 모델
주요개념
- 판별문석은 예측변수나 결과변수가 범주형이든 연속형이든 잘 작동한다
- 공분산행렬을 사용하여 한 클래스와 다른 클래스에 속한 데이터들을 구분하는 선형판별함수를 계산할 수 있다
- 이 함수를 통해 각 레코드가 어떤 클래스에 속할 가중치 혹은 점수를 구한다
5.3 로지스틱 회귀
용어정리
로짓(logit) : 무한대의 범위에서 어떤 클래스에 속할 확률을 결정하는 함수
오즈(odds) : 실패(0)에 대한 성공(1) 확률의 비율
로그오즈 : 변환 모델의 응답변수 -> 이 값을 통해 확률을 계산함
<회귀 VS 분류>
| 회귀 | 분류 | |
| 입력값 | 연속값, 이산값(밤주형) | 연속값, 이산값(밤주형) |
| 출력값 | 연속값(실수형) | 이산값(범주형) |
| 모델형태 | 일반적인 함수 : y = a + bx | 이진분류 : 시그모이드 함수 다중분류 : 소프트맥스 함수 꼭 포함 |
3.1 로지스틱 반응함수와 로짓
오즈비 : 사건이 발생할 확률을 사건이 발생하지 않을 확률로 나눈 비율
로그의 기능 : 큰 수를 작을수를 바꿔줌
로그의 사용 : 분포가 왼쪽으로 치우쳐져 있을때 ( positive skewed 한 경우) 대칭하게 만들면 정규성을 보일 수 있음
*왼쪽으로 치우친 분포는 독립변수의 값이 작을수록 많은 값이 존재

* 오른쪽으로 치우진(negative skewed한 )경우는 지수함수 사용!
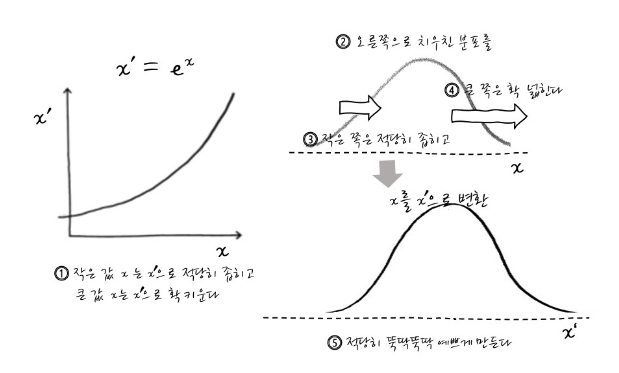
<로지스틱 함수 와 확률함수>
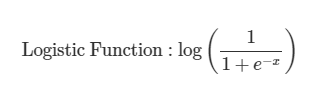
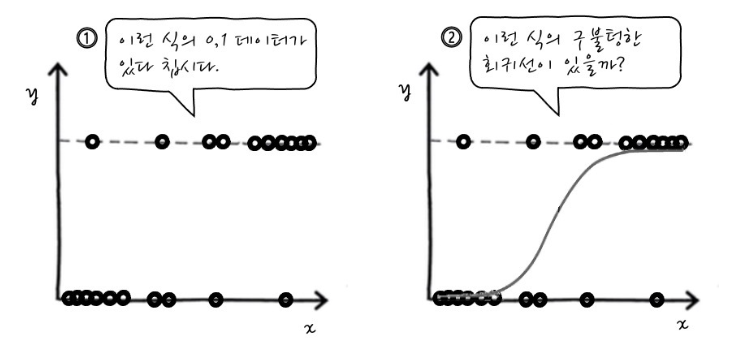
로지스틱 회귀분석의 결과는 확률값을 활용하여 회귀
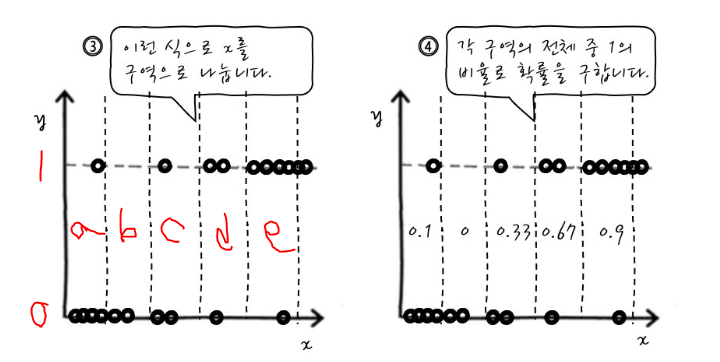
4번째 단계에서 각 구역(a~e)마다 y가 1이 나올 확률을 구하는데
a구역에서 0과1이 나온 개수중 1이 나올 개수의 확률을 구한다
1의 개수 / 0의 개수 + 1의 개수
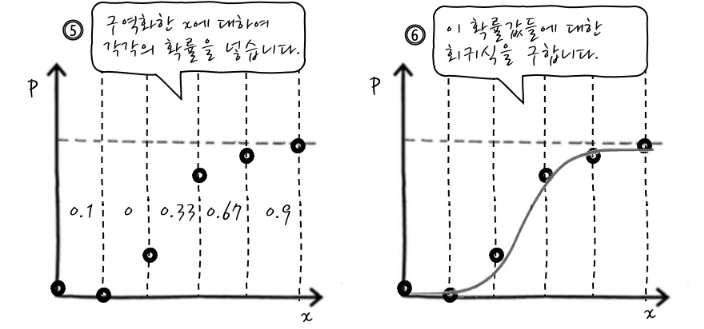
각 구역의 확률을 y값에 대입하면 독립변수에 따른 종속변수가 나올 확률(1이 나올 확률)에 대한 그래프가 된다
-> 이것이 시그모이드 함수 형태!
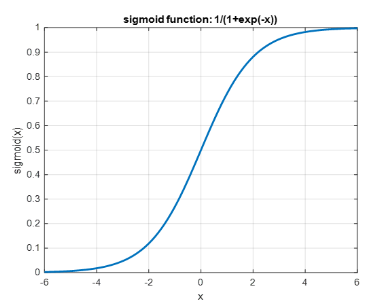
sigmoid함수 : 대략s자 곡선을 그리면서 단조롭게 증가하는 함수
sigmoid를 사용하는 이유 : 독립변수x들의 각 클래스에 대한 분포가 정규분포를 따를 것이라고 가정
x =0일때 함수의 출력값은 0.5
함수의 출력값은 항상 0이상 1이하 (중앙값은 0.5)
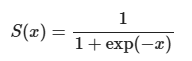 |
 |
오즈 : 성공(1)의 확률이 실패(0)의 확률에 비해 몇배 더 높은가
성공확률 + 실패확률 = 1
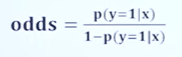
로짓변환 : 오즈에 로그를 취함으로 입력값(확률값)의 범위가 (0~1)일때 무한대를 출력함

로지스틱함수 : 로짓변환의 역함수
3.2 로지스틱 회귀와 GLM
로지스틱회귀는 선형회귀를 확정한 일반화선형모형(GLM)의 특별한 사례
'학습노트 > 통계' 카테고리의 다른 글
| 분류(3) ~ 통계적 머신러닝(1) (0) | 2024.06.17 |
|---|---|
| [통계학습] 분류 (2) (0) | 2024.06.12 |
| [통계학습] 회귀와 예측(2) (2) | 2024.06.05 |
| [통계학습] 회귀와 예측(1) (1) | 2024.06.03 |
| [통계학습] 데이터와 표본분포(3) (0) | 2024.05.29 |



