
4.5 회귀방정식 해석
- 변수 간 상관 : 변수들이 같은 방향으로 움직이려는 경향을 가짐. 예측변수(독립변수)끼리 서로 높은 상관성을 가질 때는 개별 계수를 해석하는 것이 어렵다
- -> 한 변수가 올라갈 때 다른 변수도 올라가고 그 반대 경우에도 동일
- 다중공산성 : 예측변수들이 완벽하거나 거의 완벽에 가까운 상관성을 갖는다고 할 때, 회귀는 불안정하며 계산이 불가능하다
- 교란변수 : 중요한 예측변수지만 회귀방정식에 누락되어 결과를 잘못되게 이끄는 변수
- 주효과 : 다른 변수들과 독립된, 하나의 예측변수와 결과변수 사이의 관계
- 상호작용 : 둘 이상의 예측변수와 응답변수 사이의 상호 의존적인 관계
4.5.2 다중공산성
< 다중회귀에서 다중공산성 발생원인 >

- 오류로 인해 한 변수가 여러 번 포함된 경우
- 요인변수(범주형)로부터 P-1개가 아닌 P개의 가변수가 만들어진 경우
- 두 변수가 서로 거의 완벽하게 상관성이 있는 경우
< 독립성 O >
- 변수들 간에 서로 영향을 주지 않는 것,
- 회귀 계수 b1 는 x1를 제외한 나머지 독립변수(x2, x3..)들을 고정시킨 상태에서 x1의 한 단위 증가에 따른 y의 변화를 설명
< 독립성 X >
- 독립변수들 강에 강한 상관관계가 나타나는 경우

< 문제점 >
높은 분산값으로 인해 t통계량이 낮아짐 -> 회귀계수의 유의성이 낮아짐



<원인>
변수 간에 높은 상관관계가 발생 -> 회귀분석의 수식이 복잡해짐(불안전)
= 추청치와 관측지의 오차가 커짐
(잔차가 커짐 - > t통계량이 낮아짐 -> 회귀계수 설명력 감소)
< 방안 : p-1의 사용 >
택시 데이터의 팁을 회귀분석에 적용하기 위해
color와 payment의 범주형 데이터를 원-핫 인코딩
# 범주형데이터를 원-핫인코딩으로 수치형으로 바꾸기
taxi['yellow'] = pd.get_dummies(taxi['color'], drop_first = True)
taxi['credit card'] = pd.get_dummies(taxi['payment'], drop_first = True)drop_first : 첫 번째 카테고리의 dummy 변수를 생성하지 않는다
color의 범주형에 빨강, 파랑, 초록이 있다면 파랑, 초록의 정보만 알아도 나머지는 자동으로 '빨강'임을 알 수 있음
> 1 = 빨강 + 파랑 + 초록
> y= b0 + b1(빨강) + b2(파랑) + b3(초록)
> y= b0 + b1(1 - 파랑 - 초록) + b2(파랑) + b3(초록)
> y = b0 + b1 - b1(파랑) - b1(초록) + b2(파랑) +b3(초록)
> y = b0 + b1 + (b2 - b1)(초록) + (b3 - b1)(파랑)
즉, 회귀계수들간의 상관관계 발생
* reference category 설정(기준변수 설정)
: 범주중 한개를 제거(기준변수 = 0 )하여 데이터들 간의 상관관계를 제거한 과정
| y= b0 +b1빨강 +b2파랑 +b3초록 | y= b0 +b1파랑 +b2초록 |
|
|
< 더미형 변수의 회귀계수 해석 >
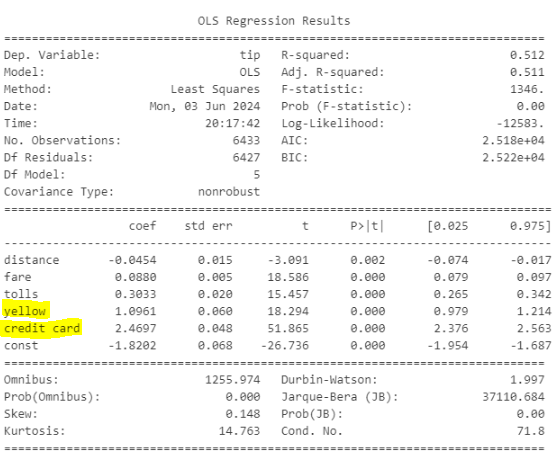
y = β0 + (-0.04)⋅distance + (0.08)⋅fare + (0.3)⋅tolls + (1.09)⋅yellow + (2.4)⋅credict card + ϵ
1. yellow + red(기준변수)
- yellow의 p값이 유의미 하다 -> yellow차량일때의 팁과 red일때의 팁이 차이가 있다
- yellow의 coef -> red일때의 팁보다 1.09 더 준다
2. credit card + cash(기준변수)
- credit card 의 p값이 유의미 하다 -> credit card 차량일때의 팁과 cash일때의 팁이 차이가 있다
- credit card의 양수 coef -> cash 일때의 팁보다 2.4 더 준다
🎈 주요개념
- 예측변수들 사이의 상관성 때문에, 다중선형회귀에서 계수들을 해석할 때는 주의해야 한다
- 다중공산성은 회귀방정식을 피팅할 때, 수치 불한정성을 유발할 수 있다
- 교란변수란 모델에서 생략된 중요한 예측변수를 의미하며 이에 따라 실제로 관계까 없는데 허위로 있는 것처럼 회귀 결과가 나올 수 있다
- 변수와 결과가 서로 의존적일 때, 두 변수 사이의 상호작용을 고려할 필요가 있다
4.6 회귀진단
- 표준화잔차 : 잔차 / 표준오차 -> 이 값을 통해 특잇값 발견
- 특잇값 : 회귀에서 특잇값은 실제 y값이 예측된 값에서 멀리 떨어진 경우
- 영향값 : 있을 때와 없을 때 회귀방정식이 큰 차이를 보이는 값
- 레버러지 : 회귀식에 한 레코드가 미치는 영향력의 정도(hat value)
- 비정규 잔차 : 정규분포를 따르지 않는 잔차는 회귀분석의 요건을 무효로 만들어 데이터 과학에서는 중요하지 않게 다룬다
- 이분산성 : 어떤 범위 내 출력값의 찬자가 매우 높은 분산을 보이는 경햔
- -> 어떤 예측변수를 회귀식이 놓치고 있다는 것을 의미할 수 있음
- 편잔차 그림 : 결과 변수와 특정 독립변수 사이의 관계를 진단하는 그림

단순회귀식의 신뢰구간과 예측구간
신뢰구간 : 평균값이 이 범위 안에 있을 가능성 > 모델이 예측한 평균값의 신뢰성
예측구간 : 실제값이 이 범위 안에 있을 가능성 > 모델이 예측한 평균값의 신뢰성
🎈 주요개념
- 특이점은 데이터 크기가 작을 때 문제를 일으킬 수 있지만, 주요 관심사는 데이터에서 문제점을 발견한다 등 이상을 찾아내는 것이다
- 데이터 크기가 작을 때는 단일 레코드(회귀 특잇값 포함)가 회귀 방정식에 큰 영행을 미치는 경우도 있다. 하지만 빅데이터에서는 대부분 이러한 효과는 사라진다
- 회귀모형을 일반적인 추론(p값)을 위해 사용할 경우 잔차 분포에 대한 특정 가정을 확인해야 한다
- > 하지만, 데이터 과학에는 잔차의 분포는 그렇게 중요하지 않다
- 편반차그림을 사용하여 각 회귀 항의 적합성을 정량적으로 평가할 수 있다. 즉, 대체 모델에 대한 아이디어를 얻을 수 있다
4.7 다항회귀와 스플라인 회귀
- 다항회귀 : 회귀모형에 다항식(제곱, 세제곱 등)항을 추가한 방식
- 스플라인 회귀 : 다항 구간들을 부드러운 곡선 형태로 피팅한다
- 매듭(Knot): 스플라인 구간을 구분하는 값들
- 일반화가법모형(GAM, generalized additive model) : 자동으로 구간을 결정하는 스플라인 모델
4.7.2 다항식
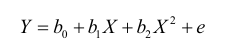
고차항을 회귀 방정식에 추가하는 것은 흔들림을 초래
-> 스플라인 : 고정된 점들 사이를 부드럽게 보정하는 방법
🎈 주요개념
- 회귀분석에서 특잇값은 잔차가 큰 레코드를 말한다
- 다중공산성은 회귀방정식을 피팅할 때 수치 불안정성을 가져올 수 있다
- 교란변수는 모델에서 생략된 중요한 예측변수이며 허위 관계를 보여주는 회귀 결과를 낳을 수 있다
- 한 변수의 효과가 다른 변수의 수준에 영향을 받는 다면 두 변수 사이의 강호작용을 고려할 항이 필요하다
- 다항회귀분석은 예측변수와 결과변수간의 비선형 관계를 검증할 수 있다
- 스플라인은 매듭들로 함께 묶여있는 일련의 구간별 다항식을 마란다
- 일반화가법모형을 사용하여 스플라인의 매듭을 자동으로 결정할 수 있다
'학습노트 > 통계' 카테고리의 다른 글
| [통계학습] 분류 (2) (0) | 2024.06.12 |
|---|---|
| [통계학습] 분류 (1) (1) | 2024.06.10 |
| [통계학습] 회귀와 예측(1) (1) | 2024.06.03 |
| [통계학습] 데이터와 표본분포(3) (0) | 2024.05.29 |
| [통계학습] 통계적실험과 유의검정(2) (0) | 2024.05.27 |



