
범위 : 4.1 단순선형회귀 ~ 4.4 회귀에서의 요인변수
4.1 단순성형회귀
- 응답변수(반응변수) : 예측하고자 하는 변수(Y, 종속변수)
- 독립변수 : 응답치를 예측하기 위해 사용되는 변수( X, 예측변수,픽처속성)
- 레코드 : 한 특정 경우게 대한 입력과 출력을 답고 있는 벡터( 행)
- 절편 : 회귀직선의 절편, X축이 0일때 Y값 -> 회귀식의 b0
- 회귀계수(regression coefficient) : 회귀직선의 기울기 -> 회귀식의 b1
- 적합값 (fitted value) : 회귀직선으로 부터 얻은 추정치(예측값)
- 잔차(residual) : 관측값과 적합값의 차이 (오차)
- 최소제곱 : 잔차의 제곱합을 최소화하여 회귀를 피팅하는 방법
- lm (limear model) :선형모델
4.1.1 회귀식
단순선형회귀를 통해 X가 얼만큼 변하면 Y가 어느정도 변화하는지 추정 가능

< 노동자들이 면진에 노출된 연수와 폐활량(peer)관계 >
import pandas as pd
url = 'https://raw.githubusercontent.com/gedeck/practical-statistics-for-data-scientists/master/data/LungDisease.csv'
lung = pd.read_csv(url)
import sklearn
from sklearn.linear_model import LinearRegression
# 독립변수, 종속변수의 넘파이 배열
predicions = lung['Exposure'].values.reshape(-1,1) # 2차원 배열
outcome = lung['PEFR'].values
model = LinearRegression() #모델생성
model.fit(predicions,outcome) #모델학습
print(f'intercept : {model.intercept_:.3f}') # 절편
print(f'coefficient exposure: {model.coef_[0]:.3f}' ) # 기울기
- intercept : 424.583
- coefficient exposure: -4.185
> 단순 회귀식 : PEFR = exposure*(-4.185) + 424.583
즉, 노동자가 면진에 노출되는 연수가 1씩 증가할 때마다 폐활량은 -4.185의 비율로 줄어든다
4.1.2 적합값(예측값)과 잔차(오차)
모든 데이터가 정확한 회귀식에 반영되지 않기 때문에 오차항 e반영
e = 실제값Y - 예측값Y^

<잔차 계산하기>
fitted = model.predict(lung[['Exposure']])
residuals = lung['PEFR'] - fitted
4.1.3. 최소제곱법 RSS
회귀선 -> 잔차들을 제곱한 값들을 합을 최소화 하는 선
* 많이 사용되는 이유 : 편의성!

🎈 주요개념
- 회귀방적식은 응답변수 Y와 예측변수 X간의 관계를 선형함수로 모델링한다
- 회귀모형은 적합값과 잔차, 즉 반응에 대한 예측과 예측 오차를 산출한다
- 회귀모형은 일반적으로 최소제곱법을 이용해 피팅한다
- 회귀는 예측과 설명 모두에 사용된다
4.2 다중선형회귀
예측변수가 여러개 일때 수식 -> 선형!

- 제곱근평균재곱오차(RMSE : root mean squares error) : 회귀시 평균제곱오차의 제곱근, 회귀모형을 평가하는 게 가장 널리 사용되는 측정 지표
- 잔차표준오차(RSE: residual standard error) : 평균제곱오차와 동일하지만 자유도에 따라 보정된 값
- R제곱 : 0에서 1까지 모델에 의해 설명된 분산의 비율 (결정계수)
- t 통계량 : 계수의 표준오차로 나눈 예측변수의 계수, 모델에서 변수의 중요도를 비교하는 기준
- 가중회귀 : 다른 가중치를 가진 레코드를 회귀하는 방법
< 회귀분석의 유의성 검정 절차 >
- 회귀 모델 선정
- 독립/종속변수 파악
- 데이터 경향성 확인
- 독립변수와 종속변수 간 산점도 분석 및 상관관계 분석을 이용하여 선형성 확인
- 회귀계수 추정
- 최소제곱법
- 최대가능도법
- 적률추정법
- 회귀계수 유의성 확인
- t검정을 이용해 회귀계수의 유의성 확인
- 독립변수 간 다중공산성 확인
- 종석변수에 영향을 주는 독립변수 선택 및 해석
- 회귀식 적합성 확인
- 모델적합성 확인 : 분산분석의 F검정
- 모델설명력 확인 : 결정계수(R^2)
- 데이터의 모델 적합성 확인 : 회귀분석의 기본가정 (정규성, 등분산성, 독립성)
- 회귀식의 영향력 진단
< 택시 데이터를 통해 팁 예측하기>
1. 회귀 모델 선정 : 수치형변수를 통해 TIP예측
import seaborn as sns
taxi = sns.load_dataset('taxis')
# 범주형데이터를 원-핫인코딩으로 수치형으로 바꾸기
taxi['yellow'] = pd.get_dummies(taxi['color'], drop_first = True)
taxi['credit card'] = pd.get_dummies(taxi['payment'], drop_first = True)
# 종속, 독립변수 구분
predictors = ['passengers','distance','fare','tolls', 'yellow', 'credit card'] #팁(종속변수)을 제외한 숫자형 데이터
outcomes = 'tip'
2. 데이터 경향성 확인
X = ['passengers','distance','fare','tolls', 'yellow', 'credit card', 'tip']
sns.pairplot(taxi[X], diag_kind='hist')
팁-거리, 요금 사이에 선형관계가 보임
단, 요금과 거리에서만 상관관계가 확인 됨
3. 회귀계수 추정
taxi_lm = LinearRegression() # 모델생성
taxi_lm.fit(taxi[predictors], taxi[outcomes]) # 모델학습
print(f'intercept:{taxi_lm.intercept_:.3f}')
print('coefficients:')
for name, coef in zip(predictors, taxi_lm.coef_):
print(f'{name}:{coef}')- intercept:-1.828 > 절편
- coefficients: > 회귀계수
- passengers:0.006
- distance:-0.045
- fare:0.088
- tolls:0.303
- yellow:1.094
- credit card:2.470
4. 회귀계수의 유의성검정 (OLS : Ordinary Leat Square)
import statsmodels.api as sm
#boolean형 데이터 수치화 -> summary()오류
taxi[['yellow','credit card']] = taxi[['yellow','credit card']].astype('int')
model = sm.OLS(taxi[outcomes], taxi[predictors].assign(const =1))
results = model.fit()
print(results.summary())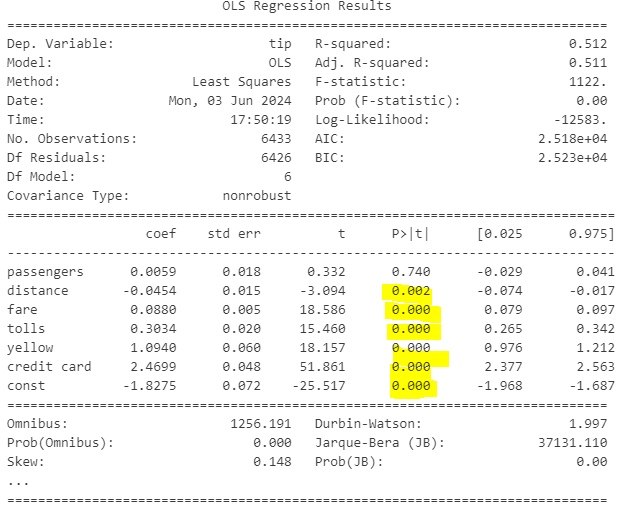
1. p-value
passanger외 변수들은 모두 유의수준 0.05보다 작으므로 회귀식의 설명력이 있다
t-통계량 = 회귀계수 추정값 / 회귀계수 표준오차
2. F-statistic
F-통계량에 대한 p-value는 유의수준 0.05보다 작으므로 모델 전체가 통계적으로 유의미하다
4.2.2 모형평가
제곱근평균제곱오차 > 모델에 대한 정확도 측정
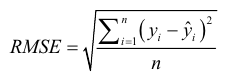
잔차표준오차 (차이점: 자유도 활용)
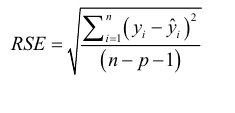
fitted = taxi_lm.predict(taxi[predictors])
RMSE = np.sqrt(mean_squared_error(taxi[outcomes], fitted))
# mean_squared_error = 실제값(taxi[outcomes]) 과 예측값(fitted)의 평균제곱오차(MSE) 구하기
# np.sqrt 제곱근 구하기
r2 = r2_score(taxi[outcomes], fitted)
print(f'RMSE:{RMSE:.0f}')
print(f'r2: {r2:.4f}')
- RMSE : 2
- r2(결젱계수) : 0.2613
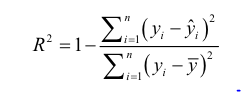
4.2.3 교차타당성 검사
다중교차타당성 검사 절차
폴드 : 훈련을 위한 샘플과 홀드아웃 샘플로 데이터를 나누는 것
- 1/k의 데이터를 홀드아웃 샘플을 따로 떼어놓는다
- 남아있는 데이터로 모델을 훈련시킨다
- 모델을 1/k 홀드아웃에 적용하고 필ㅇ한 모델평가 지표를 기록한다
- 데이터의 첫번째 1/k를 복원하고 다음 1/k을 따로 보관한다
- 2~3단계를 반복한다
- 모든 레코드가 홀드아웃 샘플로 사용될 때까지 반복한다
- 모델평가 지표들을 평균과 같은 방식으로 결합한다
4.2.4 모형 선택 및 단계적 회귀
오컴의 면도칼
변수를 추가할수록 학습데이터에 해당 RMSE는 감소하고 R^2은 증가한다
수정회귀계수
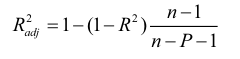
n = 레코드수, p = 모델의 변수 개수
수정R제곱을 최대로 하는 모델을 찾는 방법
1. 전진선택 : 예측변수(독립변수)없이 시작하여 각 단계에서 R^2에 가장 큰 기여도를 갖는 예측변수를 하나씩 추가하고 기여도가 통계쩍으로 더 유의미 하지 않을 때 중지
2. 후진제거 :전체 모델로 시작해서 모든 예측변수가 통계적으로 유의미한 모델이 될 때까지, 통계적으로 유의미하지 않는 예측 변수들을 제거
3. 벌점회귀 : 개별 모델 집합들을 면시적으로 검색하는 대신 모델 적합 방정식에 많은 변수(파라미터)에 대해 모델에 불이익을 주는 제약 조건을 추가(예측변수를 제거하기 보다는 크기감소 및 0으로 만들어 적용) -> 능형회귀, 라소
4.2.5 가중회귀
유용성
서로 다른 관측치를 다른 정밀도로 측정했을 때, 역분산 가중치를 얻을 수 있다 -> 분산이 높을수록 가중치가 낮다
가중치 변수가 집계된 데이터의 각 행이 나타내는 원본 관측치의 수를 인코딩하도록, 행이 여러 경우를 의마하는 데이터를 분석할 수 있다.
🎈 주요개념
- 다중선형회귀모형은 한 종속변수 Y와 여러개의 독립변수 간의 상관관계를 나타낸다
- 모델을 평가하는 가장 중요한 지표는 제곱근평균제곱오차(RMSE)와 R^2이다
- 계수들의 평균오차는 모델에 대한 변수 기여도와 신뢰도를 측정하는 데 사용된다
- 단계적 회귀 모델을 만드는 데 필요한 변수들을 자동으로 결정하는 방법이다
- 가중회귀는 방정식을 피팅할 때 레코드별로 가중치를 주기 위해 사용한다
4.3 회귀를 이용한 예측
데이터과학, 회귀의 목적은 예측
- 예측구간 prediction interval :개별 예측값 주위의 불확실 구간
- 외삽법 extrapolation :모델링에 사용된 데이터 범위를 벗어난 부분까지 모델을 확장하는 것
🎈 주요개념
- 데이터범위를 벗어나는 외삽은 오류를 유발할 수 있다
- 신뢰구간은 회귀계수 주변의 불확실성을 정량화한다
- 예측구간은 개별 예측값의 불확실성을 정량화한다
- R을 포함한 대부분의 소프트웨어는 수식을 사용하여 예측/신뢰구간을 기본 또는 지정된 출력으로 생성한다
- 예측 및 신뢰구간 생성을 위해 수식 대신 부트스트랩을 사용할 수도 있다
4.4 회귀에서의 요인변수
- 가변수 dummy variable : 회귀나 다른 모델에서 요인 데이터를 사용하기 위해 0과 1의 이진변수로 부호화한 변수
- 기준분호화 reference coding : (통계학자들이 많이 사용하는 분호화) 한 요인을 기준으로하고 다른 요인들이 이 기준에 따라 빅할 수 있도록 함
- 원핫인코딩 : 머신러닝 분야에서 많이 사용되는 부호화, 모든 요인수준이 계속 유지된다(다중선형회귀에는 부적합)
- 편차 부호화 : 기준수준과는 반대로 전체 평균에 대해 각 수준을 비교하는 부호화방법
4.4.1 가변수 선택
< taxi의 범주형 변수를 사용해서 팁 예측하기 >
predictors_c = ['color','payment'] # 번주형 변수 2개
x = pd.get_dummies(taxi[predictors_c], drop_first = True) # 다중공산성을 위해 1개씩 제거
taxi_lm_factor = LinearRegression() #모델생성
taxi_lm_factor.fit(x,taxi[outcomes]) # 모델학습
print(f'intercept : {taxi_lm_factor.intercept_:.3f}')
print('Corfficients:')
for name, coef in zip(x.columns, taxi_lm_factor.coef_):
print(f'{name}:{coef:.3f}')
intercept : -0.785
Corfficients:
color_yellow:1.004
payment_credit card:2.689
|
pd.get_dummies(taxi[predictors_c]).head()
|
pd.get_dummies(taxi[predictors_c], drop_first=True)
|
 |
 |
4.4.2 다수의 수준을 갖는 요인 변수들
-> 요소를 일부 통합하는 방법
4.4.3 순서가 있는 요인변수
🎈 주요개념
- 요인변수는 회귀를 위해 수치형 변수로 변환해야 한다
- 요인변수를 p개의 개별값으로 인코딩하기 위한 가장 흔한 방법은 p-1개의 가변수를 만들어 사용하는 것
- 다수의 수준을 갖는 요인변수의 경우, 더 적은 수의 수준을 갖는 변수가 되도록 수준들을 통합해야 한다
- 순서를 갖는 요인변수의 경우, 수치형 변수로 변환하여 사용할 수 있다
'학습노트 > 통계' 카테고리의 다른 글
| [통계학습] 분류 (1) (1) | 2024.06.10 |
|---|---|
| [통계학습] 회귀와 예측(2) (2) | 2024.06.05 |
| [통계학습] 데이터와 표본분포(3) (0) | 2024.05.29 |
| [통계학습] 통계적실험과 유의검정(2) (0) | 2024.05.27 |
| [통계학습] 통계적실험과 유의검정(1) (0) | 2024.05.22 |



