범위: 3.4 통계적 유의성과 p값 ~ 3.8 분산분석

3.4 통계적 유의성 검정
통계적유의성 : 자신의 실험의 결과가 우연히 일어난 것인지 아니면 우연히 일어날 수 없는 극단적인 것인지를 판단하는 방법
P-value : 귀무가설을 구체화한 기회모델이 주어졌을때 관측된 결과와 같이 특이하거나 극단적인 결과를 얻을 확률
alpha : 실제 결과가 통계적으로 의미있는 것으로 간주되기 위해, 우연에 의한 결과가 능가해야 하는 '비정상적인' 가능성의 임계확률
제 1종오류 : 우연에 의한 효과를 실제 효과라고 잘못 결론을 내리는 것
제 2종오류 : 실제 효과를 우연에 의한 효과라고 잘못 결론을 내리는 것
<전자상거래 실험 결과>
| 결과 | 가격 A | 가격 B |
| 전환 O | 200 | 182 |
| 전환 X | 23,539 | 22,406 |
결과 : 가격A는 가격 B에 비해 5% 우수한 결과
-> A의 전환율 = 200/(23539+200)*100 = 0.8425 %
-> B의 전환율 = 182/(22406+182)*100 = 0.8057%
검증 : 전자상거래 실험 결과가 통계적으로 유의미 한 것인가(우연이 아닌가?)
-> 귀무가설 : 가격A와 가격B간의 전환율에 차이가 없다
-> 순열검정 : 두 가격이 동일한 전환율을 공유하는지, 이 랜덤변이가 5%만큼의 차이를 만들어 낼 수 있는지 질이
# 순열검정 코드
def perm_fun(x, na, nb):
n = na + nb
# perm_fun 함수는 비복원추출방식으로 nb개의표본을 추출하고 그룹 b에 해당한다.
idx_B = list(set(random.sample(range(n),nb)))
# 그리고 나머지 na개는 그룹A에 해당한다
idx_A = list(set(range(n))- set(idx_B))
# 이때 두 평균의 차이를 결과로 반환한다
return x.loc[idx_B].mean() - x.loc[idx_A].mean()
cvr_diff = 100*(200/23739 - 182/22588)
print(f'observed difference : {cvr_diff:.4f}%')
conversion = [0]*45945 #전환되지 않은 45945개 : 값이 0인 45945개(길이)의 리스트 생성
conversion.extend([1]*382) #전환된 382개 : conversion리스트에다 값이 1인 382개 추가
conversion = pd.Series(conversion) # 리스트를 시리즈로 저장
perm_diffs = [100*perm_fun(conversion,23739,22588) # 그룹A는 23739개로, 그룹 B는 22588로 비복원 추출해서 두 평균의 차이 1000개를 저장한다
for _ in range(1000)]
fig,ax = plt.subplots(figsize = (5,5))
ax.hist(perm_diffs, bins=11, rwidth= 0.9)
ax.axvline(x=cvr_diff, color = 'pink', lw=2)
ax.text(0.06, 200, 'observed/ndifference')

np.mean([diff > cvr_diff for diff in perm_diffs])
# 순열검정을 통한 결과가 관측된 결과보다 클 확률0.324으로 유연히 얻은 결과가 30%정도 관측한 것과 비슷한 정도로 예외적인 결과로 얻을 것으로 기대한다
-> 관측된 결과보가 랜덤모델에거 극단값이 나올 확률이 30%
-> 귀무가설 채택
<전자상거래 실험 결과>는 전환, 비전환이라는 두가지 결과로 가설이 이항분포를 따르기 때문에 순열검정을 할 필요가 없다
-> 정규근사법을 통해 카이제곱 검정
* 정규근사법이란 이는 모집단이 무한하고 표본의 크기가 클 경우, 표본평균의 분포가 정규분포에 가까워지는 성질을 이용하여 이항분포와 같은 이산확률분포를 정규분포로 근사하는 방법
** 카이제곱 검정은 범주형 데이터에서 두 집단 간의 차이가 통계적으로 유의한지 확인하는 방법
# 카이제곱검정
from scipy.stats import chisquare
rate = np.array([[200,23739-200],[182,22588-182]])
# 관찰빈도 : 23739-200개중 200개 , 22588-182개중 182개
chi2, p_value, df,_ = stats.chi2_contingency(rate)
# stats.chi2_contingency -> 카이제곱통계량, p-value, 자유도, 기대빈도 출력
print(f'p-value for single sided test: {p_value/2:.4f}')
# p_value/2 단측검정(소수점 4자리까지)p-value for single stided test: 0.3498
카이제곱검정결과 순열검정과 결과가 유사함
1) 유의수준 = 임계값 = 알파
유의수준(임계값) : 제 1종오류를 범할 확률, 귀무가설이 옳은데도 불구하고 이를 기각하는 확률의 크기
신뢰도(1-유의수준) : 제 1종 오류를 범하지 않을 확률, 검정하려는 귀무가설이 참일경우, 이를 옳다고 판단하는 확률

2) P-value의 참 의미
- P-value : 랜덤모델이 주어졌을 때, 그 결과가 관측된 결과보다 더 극단적일 확률
- p값은 이 데이터가 특정 통계모델과 얼마나 상반되는지 나타낼 수 있다
- P값은 연구가설이 사실이 확률이나, 데이터가 랜덤하기 생성되었을 때 확률을 측정하는 것이 아니다
- 과학적 결론, 비즈니스나 정책 결정은 P값이 특정 임계삾을 통과하는지 여부를 기준으로 해서는 안된다
- P값 또는 통계적 유의성은 효과의 크기나 결과의 중요성을 의미하지 않는다
- P값 그 자체는 모델이나 가설에 대한 증거를 측정하기 위한 좋은 지표는 아니다
3) 가설검정의 종류
| 양측검정 | 좌측검정 | 우측검정 | |
| 귀무가설 | 모수가 특정값이다 | 모수가 특정값이다 | 모수가 특정값이다 |
| 대립가설 | 모수가 특정값이 아니다 | 모수가 특정값 보다 작다 | 모수가 특정값 보다 크다 |
| 그래프 |  |
 |
 |
4) 통계적 가설검정 절차
검정통계량 : 귀모가설과 대립가설 중에서 하나의 가설을 선택하는데 사용하는 표본의 통계량
예) Z통계량, t통계량, 카이제곱통계량, F통계량의 확률분포상의 x축 좌표
기각역 : 가설검정에서 유의수준 a가 정해졌을때 검정통계량의 분포에서 이 유의수준의 크기에 해당하는 영역(귀무가설 기각)
채택역 : 검정통계량의 분포에서 이 유의수준을 제외하는 크기에 해당하는 영역(귀무가설 채택)
| 가각역사용(가설설정) | P값 사용(유의성검정) | |
| 1단계 | 가설을 설정하고 대립가설에 따라 단측/양측 검정방법을 선택한다 | |
| 2단계 | 유의수준 결정 | |
| 3단계 | 검정통계량 선정 및 계산 | |
| 4단계 | 표본의크기n과 유의수준에 따른 기각역 설정 | 검정통계량을 사용하여 P값 산출 |
| 5단계 | 통계적결론 -> 검정통계량이 기각역에 속하면 귀무가설 기각, 아닌경우 귀무가설 채택 > 검정통계량과 t값 비교 |
통계적결론 -> 유의수준이 P값보다 크면 귀무가설 기각, 아닌경우 채택 > 유의수준과 P값 비교 |
<성별에 따른 가입자수 상관관계 구하기 >
* 카이제곱 검정 이유 : 두 개의 범주형 변수(실험대상 여부, 성별)의 관련성을 알고자함
1단계
귀무가설 : 2024-01-11 이전에 가입한 고객(대조군)과 이후에 가입한 고객(실험군)의 성비에는 차이가 없을 것이다
-> 양측검정
2단계
유의수준 0.05
3단계
# 실험군: 2024 신규 유입 유저
treatment = df[df.account_created_at >= '2024-01-11'].copy()
# 대조군: 기존 유저
control = df[df.account_created_at < '2024-01-11'].copy()
# 실험군의 성별 가입자수
test_F = treatment[treatment['gender']=='M']['user_id'].nunique()
test_M = treatment[treatment['gender']=='F']['user_id'].nunique()
# 대조군의 성별 가입자수
cont_F = control[control['gender']=='M']['user_id'].nunique()
cont_M = control[control['gender']=='F']['user_id'].nunique()
## Part1. Chi-square Test Report
genderF = [test_F, cont_F] # A와 B의 여성 유저 수
genderM = [test_M, cont_M] # A와 B의 남성 유저 수
## Part2. Contingency Table & Chi-squaure Model
## 기초 테이블 형성
cont_table = pd.DataFrame([genderF,genderM], columns=['treatment', 'control'], index=['F','M'])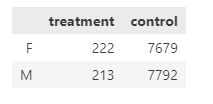
## Part3. 카이제곱 독립성 검정 모델 선언
chi2, p_val, d_f, expected = chi2_contingency([genderF,genderM])
## 기대값 표 형성
ex = pd.DataFrame(expected, columns = ['treatment', 'control'], index = ['F','M'])
print( ' '
, '[Chi-square Analysis Result Report]'
, 'Chi-square: {}'.format(round(chi2, 2))
, 'P-value: {}'.format(round(p_val, 2))
, '--------------------------'
, 'Expected Values'
, ex
, '--------------------------'
, 'Observed Values'
, cont_table
, '=========================='
, ' '
, sep = '\n')[Chi-square Analysis Result Report]
Chi-square: 0.28 P-value: 0.6
| 기각역사용(가설설정) | P값 사용(유의성검정 : 0.05) | |
| 4단계 | 기각역은 자유도1, 유의수준 0.025하에서 카이제곱분포도에 따라 5.024 *양측검정이므로 0.5/2 수준의 t값 |
카이제곱 검정에 따라 P값은 0.6 |
| 5단계 | 카이제곱통계량은 0.28으로 5.024 보다 작아 채택역에 포함된다 |
0.6은 유의수준 0.05보다 크므로 귀무가설을 채택한다 |


3.5 T검정
검정통계량 : 관심의차이 또는 효과에 대한 측정 지표
t통계량 : 평균과 같이 표준화된 형태의 일반적인 검정통계량
t분포 : 관측된 t통계량을 비교할 수 있는 기준 분포
목적 : 두 집단의 평균값이 같은지 다른지 알고싶음

두 표본 그룹 평균의 차이가 어느정도 커야 크다고 할 수 있을까?(우연이 아니라고 할 수 있을까?)
방법 : 표준편차
> 두 집단의 평균의 차이가 표분편차보다 작다면 두 집단의 평균의 차이는 우연히 발생한 것
특징
표본의 크기 n이 커지면 t값이 커지고, t분포는 표준정규분포에 근사한다
t-test에서 자유도는 n-1로 계산되므로, 표본의 크기가 커지면 커자유도가 커지고, 자유도가 커지면 표준정규분포를 사용할 수 있음
| one sample t-test 귀무가설 : 표본의 평균과 모집단은 동일할 것이다 paired t-test 귀무가설 : 표본의 실험전 평균과 실험후 평균은 동일할 것이다 |
two sample t-test *분모계산이 어려움 https://angeloyeo.github.io/2020/02/13/Students_t_test.html |
 |
  |
< t검정 사례 : 이번달 평균 재조량이 기존 평균이랑 동일한가? >
사례 : 어느 공장에서 관리자가 원재료 리터당 제품이 500g씩 제조된다고 주장한다.
이를 입증하기 위해 19개의 표본을 추출결과 표본평균이 518g이고 표준편차가 40g일때
신뢰수준 0.05하에서의 결론
귀무가설 : 이번달 리터당 평균 재조량은 기존 500g과 동일할 것이다
표본의 수 n =19, 자유도 = 18
T 통계량 = 518 - 500 / 40√20 = 1.9615
결론 : 계산된 t통계량이 신뢰수준 안에 있으므로( 1.9615 < 2.101 ) 귀무가설 채택
-> 리터당 제품이 500g씩 제조된다고 할 수 있음
* 유의수준을 활용하면 t값은 자유도18, 유의수준0.025에서 t값은 2.101이르로 귀무가설을 채택한다


🎈 t통계량과 t값의 차이
t통계량은 표본 데이터로부터 계산되는 반면, t값은 유의수준과 자유도에 따라 결정
- 계산된 t통계량의 절대값이 t분포표의 t값보다 크면 귀무가설을 기각.
- 계산된 t통계량의 절대값이 t분포표의 t값보다 작으면 귀무가설을 채택
3.6 다중검정
1종오류 : 어떤 효과가 통계적으로 유의미하다고 잘못된 결론을 내린다
거짓발견비율(FDR) : 다중검정에서 1종 오류가 발생하는 비율
알파인플레이션 : 1종오류를 만들 확률인 알파가 더 많은 데스트를 수행할수록 증가하는 다중검정현상
P값 조정 : 동일한 데이터에 대해 다중검정을 수행하는 경우 필요
과대적합: 잡음까지 피팅
🎈 주요개념
- 연구조사나 데이터 마이닐 프로젝트에거 다중성(다중비교, 많은 변수, 많은모델)은 일부가 우연히 유의미하다는 결론을 내릴 위험을 증가시킨다
- 여러 통계비교(여러 유의성 검정)와 관련된 상황의 경우 통계적 수정 절차가 필요하다
- 데이터마이닝에서, 라벨이 지정된 결과변수가 있는(즉 분류결과를 알고 있는)홀드아웃표본을 사용하면 잘못된 결과를 피할 수 있다
3.7 자유도
자유도 : 표본데이터에서 계산된 통계량에 적용하면 변화가 가능한 값들의 개수
표본크기 n : 해당 데이터에서 관측값의 개수(행, 기록값)
🎈 주요개념
자유도는 검정통계량을 표준화하는 계산의 일부이며, 이를 통해 기준분포(t분포,F분포) 와 비교할 수 있다
자유도 개념은 회귀 할 때 다중공산성을피하기 위해 범주형 변수들을 n-1지표 혹은 더미 변수로 요인화하는 것의 이유가 된다
3.8 분산분석
쌍별비교 pairwise comparison : 여러 그룹 중 두 그룹간의 가설검정
총괄검정 omnibus test : 여러 그룹 평균들의 전체 분산에 대한 단일 가설검정
반산 분해 : 구성 요소 분리( 전체 평균, 처리평균, 잔차 오차로부터 개별 값들에 대한 기여)
F통계량 : 그룹 평균 간의 차이가 랜덤 보델에서 예상되는 것에사 밧아나는 정도를 측정하는 표준화된 통계량
(잔차 오차로 인한 분산과 그룹 평슌의 분산에 대한 기초)
ss(sum of squares) : 어떤 평균으로부터의 편차들의 제곱합
🎈 주요개념
ANOVA는 여러 그룹의 실험 결과를 분석하기 위한 통계쩍 절차이다
A/B 검정과 비슷한 절차를 확장하여 그룹 간 전체적인 편차가 우연히 발생할 수 있는 범위 내에 있는지를 평가하기 위해 사용한다
ANOVA의 결과 중 유용한 점 중 하나는 그룹처리, 상호작용효과, 오차와 관련된 분산의 구성 요서들을 구분하는데 있다
'학습노트 > 통계' 카테고리의 다른 글
| [통계학습] 회귀와 예측(1) (1) | 2024.06.03 |
|---|---|
| [통계학습] 데이터와 표본분포(3) (0) | 2024.05.29 |
| [통계학습] 통계적실험과 유의검정(1) (0) | 2024.05.22 |
| [통계학습] 데이터와 표본분포(3) (2) | 2024.05.20 |
| [통계학습] 데이터와 표본분포(2) (0) | 2024.05.14 |



