
범위 2.4 부트스트랩 ~ 2.8 스튜던트의 T분포
2.4 부트스트랩
모수의 표본분포를 추정하는 효과적인 방법으로 표본을 복원추출하여 통계량과 모델을 다시 계산하는 것
-> 데이터나 표본통계량이 정규분포를 따를필요 없음
-> 복원추출 장점: 원소가 뽑힐 확율을 그대로 유지하면서 큰 모집단 형성 가능
부트스트랩 표본: 관측데이터 집합으로부터 얻은 복원추출
재표본추출(재표집, 리샘플링) : 관측데이터로부터 반복해서 표본을 추출하는 과정(여러표본이 결합되어 비복원추출을 수행할 수 있는 순열과정을 포함)
*부트스트랩은 항상 관측된 데이터로부터 복원추출
1) 부트스트랩 알고리즘
- 샘플값을 하나 뽑아서 기록하고 다시 제자리에 놓는다
- n번 반복
- 재표본추출된 값의 평균을 기록한다
- 1~3간계를 R번 반복한다 *반복이 많을 수록 표준오차나 신뢰구간에 대한 추정이 더 정확해진다
- R개의 결과를 사용하여 표준편차/히스토그램/신뢰구간을 구한다
2) 파이썬 resample()
# 부트스트랩
from sklearn.utils import resample
tip = tips['tip']
result =[]
for nrepeat in range(1000):
sample = resample(tip)
result.append(sample.median()) #샘플의 중간값을 삽입 *1000번
result = pd.Series(result)
print('Boostrap Statistics:')
print(f'original:{tip.median()}')
print(f'bias:{result.mean()-tip.median()}') #sample_statistics.median() - data.median())
print(f'std.error:{result.std()}')3) Boostrap Statistics
original:2.9 *원래 표본에서 중간값
bias:-0.0623800000000001 *부트스트랩 분포의 평균 - 원래표본의 중앙값
std.error:0.16880115351925004 *부트스트랩 분포의 표준편차
*(모델링에서의) 편향 계산원리
편향 : 예측값과 정답값의 차이
계산 : 제곱 -> 음수반영

해석
중간값의 원래 추정치는 2.9달러, 부트스트랩 분포는 추정치에서 약 -0.062달러 만큼의 편향이 있고
약 0.17달러만큼의 표준오차가 있는 것으로 나타난다
3) 부트스트랩 활용
- 모델성능평가 : 모델의 성능 지표(정확도, F1-score 등)에 대한 신뢰구간을 계산하는 데 활용
- 과적합 방지: 부트스트랩을 활용한 배깅(Bagging)
- 모수의 분포를 모를 때 평균의 신뢰구간을 구할 수 있음
방법: 측정된 데이터 중에서 중복을 허용하여 설정한 만큼 뽑고, 그들의 평균을 구함
-> 표본에서 복원추출로 뽑은 데이터의 평균의 분포를 통해 신뢰구간 파악
장점
(1) 모집단의 분포에 대한 가정 불필요 -> 정규분포가 아니어도 가능
(2) 표본이 작아도 신뢰구간 계산 가능
참고 : https://recipesds.tistory.com/entry/%EB%B6%80%ED%8A%B8%EC%8A%A4%ED%8A%B8%EB%9E%A9%EC%97%90-%EA%B4%80%ED%95%9C-%EC%9D%B4%EA%B2%8C-%EB%AC%B4%EC%8A%A8-%EC%86%8C%EB%A6%AC%EC%9D%B8%EA%B0%80-%ED%95%98%EB%8A%94-%EC%9D%B4%EC%95%BC%EA%B8%B0
4) 재표본추출 VS 부트스트랩핑
공통점 : 원본 데이터에서 무작위로 표본을 추출하는 방법
부트스트랩핑 ⊂ 재표본추출(resampling)
재표본추출 : 부트스트래핑(복원추출) + 순열검정(비복원추출)
*순열( : 서로다른 n개의 원소에서 r개를 중복없이 순서를 고려하여 선택하거나 나열하는 것

순열검정 : 두 개 이상의 표본을 함께 결합하여 관측값들을 무작위로 비복원하여 재표본으로 추출하고 이를 이용해서 가설을 검증하는 방법
방법
- 기존 데이터의 검정통계량을 구한다-> observed test statistics = D
- 그룹A와 그룹 B의 결과를 합친다
-> 그룹A와 그룹B가 유의미한 차이가 없다는 귀무가설을 논리적으로 구체화 하는 것 - 결합된 데이터를 섞고 그룹A와 동일한 크기(동일한 개수)의 표본을 무작위로 비복원추출한다
- 나머지 데이터에서 그룹B와 동일한 크기의 표본을 무작위로 비복원추출한다-> permuted dataset
- 원래 샘플에 대한 통계량과 무관하게 추출한 표본에 대한 통계량을 기록한다 -> permuted test statistics
- 앞선 단계들을 반복하여 검정통계량의 순열분포를 얻는다
활용 : 가설검증
단측검정 : permuted test statistics가observed test statistics 보다 클/작을 확률
양측검정 : permuted test statistics의 절댓값이 observed test statistics 보다 클 확률

종류: 인의순열검정, 전체순열검정, 부트스트랩순열검정
참고1. https://velog.io/@khyun11/%ED%86%B5%EA%B3%84-%EC%9E%AC%ED%91%9C%EB%B3%B8%EC%B6%94%EC%B6%9C
[통계] 재표본추출 (부트스트랩과 순열검정)
표본을 반복적으로 추출하여, 무작위 변동성을 알아보는 것.머신러닝 모델의 정확성을 평가하고 향상시키기 위해 적용 가능. \- 부트스트랩 데이터 집합을 기반으로 각 표본 당 의사결정트리 예
velog.io
참고2.
https://esj205.oopy.io/0bf3f7b0-d3e0-4a0e-af64-d0b40a23b351
순열검정법(Permutation Test)
1. 정의
esj205.oopy.io
🎈 주요개념
- 부트스트랩은 표본통계량의 변동성을 평가하는 강력한 도구
- 부트스트랩은 수학적 근사가 어려운 통계량에서도 샘플링 분포 추청이 가능
- 예측 모델시 여러 부트스트랩 표본들로부터 얻은 예측값을 모아서 결론을 만드는 것(배깅)이 단일 모델보다 좋다
2.5 신뢰구간
신뢰수준: 같은 모집단으로부터 같은 방식으로 얻은, 관심 통계량을 포함할 것으로 예상되는 신뢰구간의 백분율
구간끝점 : 신뢰구간의 최상위, 최하위 끝점
1) 90% 신뢰구간
= 표본통계량의 부트스트랩 표본분포의 90%를 포함하는 구간
= 평균적으로 유사한 표본추정치 90%정도가 포함
= 모집단의 모수(평균 등)가 해당 구간에 포함될 확률
= [x̄ - 1.645 × SE, x̄ + 1.645 × SE] -> 1.645 : 표준정규분포의 90%신뢰수중에 해당하는 z값
= z=0에서 z=1.645까지의 면적 0.45(음의 영역도 0.45로 두개 합이 0.90)
| z-score | 정규분포 |
 |
 |
참고1. https://mathblog.com/statistics/definitions/z-score/ci/90-to-z/
90% Confidence Interval to Z-score
A 90% confidence interval conveys a 90% likelihood that the true population parameter is encompassed within our determined range. This level yields greater assurance compared to an 80% confidence interval but is less stringent than the 95% confidence level
mathblog.com
참고2. https://blog.naver.com/aporia25/221154921293
2) 부트스트랩을 통한 신뢰구간 구하기
- 데이터에서 복원 추출 방식으로 크기 n인 표본을 뽑는다(재표본추출)
- 재표본추출한 표본에 대해 원하는 통계량을 기록한다
- 1~2단계를 R번 반복한다
- x% 신뢰구간을 구하기 위해, R개의 재표본 결과의 분포 양쪽 끝에서[(100-x)/2]%만큼 잘라낸다
- 절단한 점들은 x%부트스트랩 신뢰구간의 양 끝점이다
🎈 주요개념
- 신뢰구간은 구간 범위로 추정값을 표시하는 일반적인 방법이다.
- 더 많은 데이터를 보유할수록 표본 추정치 변이가 줄어든다
- 허용할 수 있는 신뢰수준이 낮을 수록 신뢰구간은 좁아진다
- 부트스트랩은 신뢰구간을 구성하는 표과적인 방법이다
2.6 정규분포
오차 : 데이터 포인트와 예측값 혹은 평균 사이의 차이
표준화(정규화) standardize : 평균을 빼고 표준편차로 나눈다
z-score :개별 데이터포인트를 정규화한 결과
표준정규분포 : 평균=0, 표준편차 =1인 정규분포(x축 단위 = 평균의 표준편차)
QQ그림 : 표본분포가 특정 분포(정규분포)에 얼마나 가까운지 보여주는 그림

1) 표준정규분포와 QQ그림
QQ plot원리 : https://diseny.tistory.com/entry/QQ-Plot-%EA%B7%B8%EB%A6%AC%EA%B8%B0-%EB%B0%8F-%ED%99%9C%EC%9A%A9%EB%B2%95
QQ Plot 직관적으로 이해하기
1. 기본 개념 QQ 플롯(Quantile-Quantile Plot)의 Quantile은 분위수라는 의미인데, 분위수는 데이터를 오름차순(내림차순)정렬한 뒤, 전체 데이터를 특정 개수로 나눌 때 기준이 되는 수다. 예를 들어 4분
diseny.tistory.com
QQ그림 : Z점수를 오름차순으로 정렬하고 각 값의z점수를 y축에 표시(책 :92P) -> y축이 각 데이터의 Z-score인가??

의미 : 두 확률분포를 비교하는 그래프, 주로 데이터가 특정 이론적 분포(예: 정규분포)를 따르는지 확인하는 데 사용
-> X축 : 정규분포에서의 해당 분위수
-> Y축 : 실제 데이터의 분위수(quantile)
-> 단위 : 평균으로부터 떨어진 데이터의 표준편차 수
-> 해석 : 점들이 대략 대각선위에 놓이면 정규분포에 가까운 것
*분위수: 데이터의 분포에서 전체 넓이를 일정 비로 나누어 위치에 있는 값
# 표준화 : 변수 각각의 평균을 0, 분산을 1로 만들어주는 스케일링 -> 표준정규분포
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
bill = tips['total_bill']
bill_df = pd.DataFrame(bill)
bill_std = scaler.fit_transform(bill_df).ravel()
# .fit_transform(데이터프레임)
# stats.probplot(1차원array) -> ravel() : 다차원을 1차원으로 번경
# QQ그림
import scipy.stats as stats
fig,ax = plt.subplots(figsize=(4,4))
stats.probplot(bill_std, plot=ax)
# 정규화 하지 않은 경우 QQ그림
fig,ax = plt.subplots(figsize=(4,4))
bill_org = tips['total_bill'].ravel()
stats.probplot(bill_org, plot=ax)| 정규화한 데이터 | 정규화 하지 않은 데이터 |
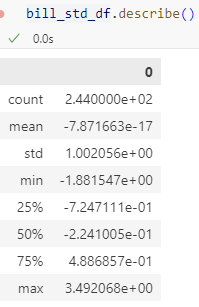 *-7.871663e-17 = -0.000000000000000079(0의 근사값) |
 |
 |
 |
 |
 |
QQplot해석: 낮거나 높은 값의 점들이 대각선보다 높은 위치에 존재하여 정규분포를 따르지 않는다
+ 양의 왜도
| 음의 왜도 | 양의 왜도 |
 |
 |
참고: https://velog.io/@yuns_u/QQ-plot-%ED%95%B4%EC%84%9D%ED%95%98%EA%B8%B0
1. 정규화를 하지 않아도 X축은 정규분포에 해당하는 분위수를 나타내는가?
-> 답 : QQplot은 데이터를 표준정규분포하여 그리는 그림
2. 정규화를 하거나 하지 않아도 분포는 동일한가
-> 의문의 이유 : 정규분포형태로 만들기 위해 정규화를 하는데 달라진 점이 없음.....
-> YES :표준화는 데이터의 단위를 제거하는 것으로 분포가 달라지지 않는다
3. Y축 실제 데이터의 분위수(quantile)의 의미..? : x축의 데이터 분포( QQ plot데이터 원리 참고)
*부트스트랩을 통한 표본의 QQ plot
# 부트스트랩의 QQplot
total_bill = tips['total_bill']
result =[]
for nrepeat in range(1000):
sample = resample(total_bill)
result.append(sample.median())
bill_result = pd.Series(result)
fig,ax = plt.subplots(figsize=(4,4))
bill_resurt_qq = bill_result.ravel()
stats.probplot(bill_resurt_qq, plot=ax)| 히스토그램 | 기초통계량 | qq plot |
 |
 |
 |
-> 원래의 데이터보다 더 정규분포의 형태를 이룸
🎈 주요개념
- 정규분포는 불확실성과 변동성에 관한 수학적 근사가 가능하게 함
- 원시 데이터 자체는 대개 정규분포가 아니지만, 표본들의 평균과 합계, 오차는 많은 경우 정규분포를 따른다
- 데이터를 Z점수로 변환하려면 데이터의 값에서 평균을 빼고 표준편차로 나눈다
2.7 긴꼬리분포
꼬리 tail : 적은 수의 극단값이 존재하는, 도수분포의 길고 좁은 부분 -> 극단값
왜도 skewmess : 분포의 한쪽꼬리가 반대쪽 다른 꼬리보다 긴 정도
🎈 주요개념
- 대부분의 데이터는 정규분포를 따르지 않는다
- 정규분포를 따를 것이라는 가정은 자주 일어나지 않는 경우(흑고니?)에 관한 과소평가를 가져올 수 있다
2.8 스튜던트 t 분포
n : 표본크기
자유도 : 다른 표본크기, 통계량, 그룹수에 따라 t분포를 조절하는 변수
🎈 주요개념
- t분포는 정규분포와 비슷한데 꼬리만 조금 더 두꺼운 형태이다
- t분포는 표본평균, 두 표본평균 사이의 차이, 회귀파라미터 등의 분포를 위한 기준으로 널리 사용
'학습노트 > 통계' 카테고리의 다른 글
| [통계학습] 통계적실험과 유의검정(1) (0) | 2024.05.22 |
|---|---|
| [통계학습] 데이터와 표본분포(3) (2) | 2024.05.20 |
| [학습노트] 통계2. 데이터와 표본분포 (1) (0) | 2024.04.01 |
| [학습노트] 통계1. 탐색적 데이터 분석 (0) | 2024.04.01 |
| [강의노트] 통계 - 통계적 가설검정, p-value (1) | 2024.01.22 |



