
위치추정 : 데이터의 대부분의 값이 어디에 있을까?(대표성)
평균 : 모든 값의 총합을 개수로 나눈 값
가중평균 : 가중치를 곱한 값의 총합을 가중치의 총합으로 나눈 값
중앙값(중간값) : 데이터에서 가장 가운데 위치한 값
백분위수 : 전체 데이처의 P%를 아래에 두는 값(= 분위수)
가중 중앙값 : 데이터를 정렬한 후, 각 가중치 값을 위에서부터 더할 때, 총합의 중간이 위치하는 값
절사평균 : 정해진 개수의 극단값을 제외한 나머지 값들의 평균
로버스트하다 : 극단값들에 민감하지 않는다는 것을 의미(=저항성이 있다)
특이값 : 대부분의 값과 매우 다른 데이터의 값
참고: https://dacon.io/en/competitions/official/235901/codeshare/5085
import pandas as pd
import scipy.stats
import numpy as np
state = pd.read_csv('https://raw.githubusercontent.com/gedeck/practical-statistics-for-data-scientists/master/data/state.csv')
# 산술평균 -> 6162876.3
state['Population'].mean()
# 절사평균 구하기 -> 4783697.125
from scipy import stats
stats.trim_mean(state['Population'],0.1)
#0.1 -> 각 끝에서 10% 제외
# 중앙값 -> 4436369.5
state['Population'].median()
# 넘파이를 활용한 가중평균 -> 살인율을 인구에 가중치를 더해서 평균을 구함 -> 4.445833981123393
np.average(state['Murder.Rate'], weights = state['Population'])
상하위 10%를 제외한 절사평균과 중앙값이 비슷하고 산술평균이 2,000,000정도 더 커지기 때문에 극단값이 크다
또한 중앙값이 평균보다 작기때문에 오른쪽으로 치우친 그래프, 양의 왜도를 가짐
- 가장 기본적인 위치추정은 평균이다, 그러나 극단값에 민간
- 중간값, 절사평균과 같은 방법으리 특잇값이나 이상데이터로부터 좀더 로버스트하다
변이추청 : 데이터가 얼마나 밀집해 있을까?
가정 : 데이터가 정규분포를 따름
편차 : 관측값과 위치 추정값 사이의 차이(오차, 잔차)
분산 : 평균과의 편차를 제곱한 값들의 합을 n-1로 나눈값
-> 표준편차는 표본의 평균에 따른다는 하나의 제약조건을 가지고 있기 때문에 n-1의 자유도를 갖는다
표준편차 : 분산의 제곱근
평균절대편차 : 평균과의 평차의 절대값의 평균(맨해튼 노름)
중간값의 중위절대편차(MAD) : 중간값과의 편차의 절대값의 중간값
여기서 은 데이터의 중위값,상치에 대해 덜 민감
범위 : 데이터의 최댓값과 최솟값의 차이
순서통계량 : 최소에서 최대까지 정렬된 데이터 값에 따른 계량형
백분위수 : 어떤 값들의 P퍼센트가 이 값 혹은 더 작은 값을 갖고 (100-P)퍼센트가 이 값 혹은 더 큰 값을 갖도록 하는 값
사분위범위 : 75번째 백분위수와 25번쨰 백분위수 사이의 차이
# 표준편차 -> 6848235.347401142
state['Population'].std()
# 사분위범위 -> 4847308.0
state['Population'].quantile(0.75) - state['Population'].quantile(0.25)
# 중위절대편차 -> 3849876.1459979336
import statsmodels.api as sm
sm.robust.scale.mad(state['Population'])
# 중위절대편차는 특잇값에 영향을 받지 않이 때문에 표준편차보다 값이 작다
- 분산과 표준편차는 가장 보편적인 변이 측정 방법 -> 모두 특잇값에 민감
- 중간값과 백분위수로부터 평균 절대편차와 중간값의 중위절대편차를 구하는 것이 로버스트 함
데이터 분포
도수분포표 : 동일한 구간(bin)에 해당하는 수치 데이터 값들의 빈도를 나타내는 기록( 각 구간마다 몇개의 변숫값이 존재하는가)
히스토그램 : X축은 구간들을, Y축은 빈도수를 나타내는 도수테이블 그림(막대그래프X)
밀도그림 : 히스토그램(데이터의 분포)를 부드러운 곡선으로 그린 그림
# 살인율의 백분위 수
state['Murder.Rate'].quantile([0.05, 0.25, 0.5, 0.75, 0.95])
# 박스플랏
ax = (state['Population']/1000000).plot.box()
ax.set_ylabel('population(millions)')
# 도수분포표
# pandas.cut -> 이 값들을 각 구간에 매핑하는 시리즈를 만든다
# value_counts 매서드 -> 빈도 제이블을 구함
binnedpopulation = pd.cut(state['Population'], 10) # 10개의 동일한 구간으로 만듧
binnedpopulation.value_counts()
# 히스토그램
ax2 = (state['Population']/1000000).plot.hist(figsize =(4,4))
ax.set_xlabel('Popluation')
# 밀도 그림
ax3 = state['Murder.Rate'].plot.hist(density = True, xlim=[0,12], bins =range(1,12))
state['Murder.Rate'].plot.density(ax=ax3)
ax3.set_xlabel('Merder Rate (per 100,000)')
- 도수 히스토그램은 Y축에 횟수를 X축에 변숫값들을 표시
- 도수분포표는 히스토그램에 보이는 횟수들을 표 형태로 나타낸 것
- 상자그림에서 상자의 위와 아래 부분은 각 75%, 25% 백분위수를 의미
이진데이터 VS 범주데이터
최빈값 : 데이터에서 가장 자주 등장하는 범주/값
기댓값 : 범주에 해당하는 어떤 수치가 있을때, 범주의 출연 확률에 따른 평균
-> 계산: 각 결과값에 발생확률을 곱하고 모두 더한다 (= 가중평균)
막대도표 : 각 범주의 빈도수 혹은 비율을 막대로 나타낸 그림
-> 히스토그램의 x축은 수치적으로 나타낼 수 있는 하나의 변수로 서로 붙어 있고, 막대그래프는 서로다른 범주로 떨어져있음
파이그림 : 각 범주의 빈도수 혹은 원의 부채꼴 모양으로 나타낸 그림
- 범주형데이터는 보통 비율로 요약하고 막대그래프를 사용
- 범주란 전혀 다른 집합(사과, 오렌지, 남자, 여자)정도를 나타내는 요인변수의 수준, 구간별로 나뉨 수치 데이터 같은 것을 의미
- 기댓값은 어떤 값과 그 값이 일어날 확률을 서로 곱해 더한 값 -> 요인변수의 수준을 요약
상관관계
상관계수 : 수치적 변수들 간에 어떤 관계가 있는지를 나타내기 위해 사용되는 측정량(-1~1)
-> 변수1,2 각각의 평균으로 부터 편차들을 서로 곱한 값의 평을각 변수의 표분편차의 곱으로 나누어줌
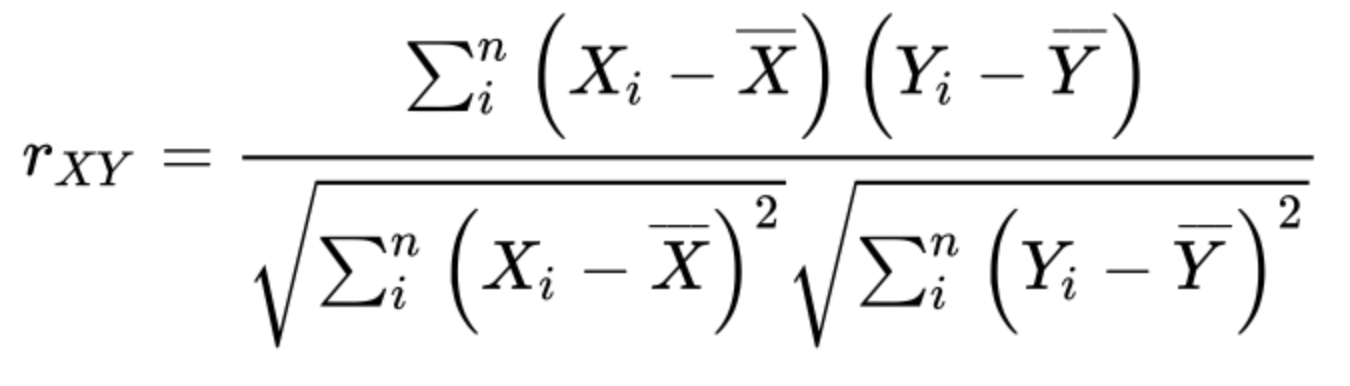
상관행렬 : 행과 열이 변수들을 의미하는 표, 각 셀은 그 행과 열에 해당하는 변수들간의 상관관계
산점도 : X축과 Y축이 서로 다른 두 개의 변수를 나타내는 도표
import seaborn as sns
etfs = sp500_px.loc[sp500_px.index > '2012-07-01',
sp500_sym[sp500_sym['sector'] == 'etf']['symbol']]
sns.heatmap(etfs.corr(), vmin =-1, vmax = 1,
cmap=sns.diverging_palette(20,220,as_cmap = True))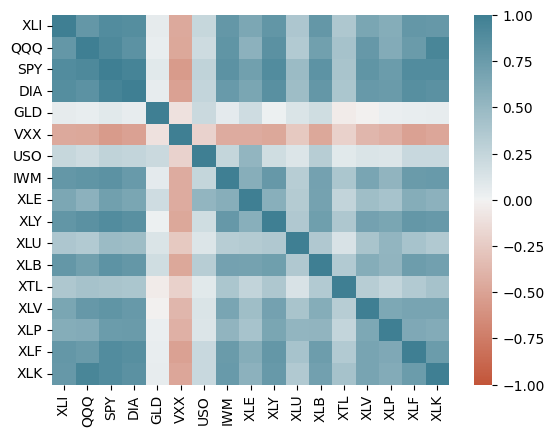
# 산점도 그리기
AA = sp500_px[['QQQ','XLK']]
ax = AA.plot.scatter(x= 'QQQ', y = 'XLK', figsize = (4,4))
ax.axhline(0, color = 'grey', lw =1) # 수평보조선
ax.axvline(0, color = 'grey', lw =1) # 수직보조선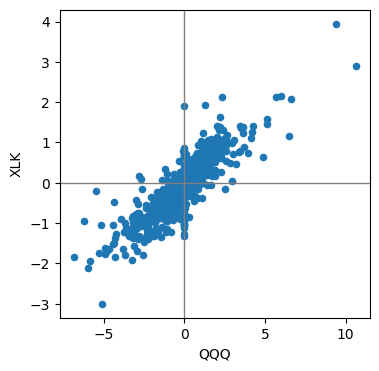
- 상관계수는 두 사이에 어떤 관계가 있는지 측정(-1~1, 사이의 값으로 0이면 관계x)
여러개의 변수 탐색
일변량분석 = 하나의 변수를 다루는 평균, 분산
이변분석량 = 상관계수처럼 두 변수를 다룸
다변량분석 : 셋 이상
분할표 : 두가지 이상의 범주형 변수의 빈도수를 기록한 표
육각형 구간 : 두 변수를 육각형 모양의 구간으로 나눈 그림
등고 도표 : 자도상에 같은 높이의 지점을 등고선으로 나타내는 것처럼, 두 변수의 밀도를 등고선으로 표시
바이올린 도표 : 상자그림과 비슷하지만 밀도 추정 추가
'학습노트 > 통계' 카테고리의 다른 글
| [통계학습] 데이터와 표본분포(2) (0) | 2024.05.14 |
|---|---|
| [학습노트] 통계2. 데이터와 표본분포 (1) (0) | 2024.04.01 |
| [강의노트] 통계 - 통계적 가설검정, p-value (1) | 2024.01.22 |
| [강의노트] 통계 - 검정통계량, ANOVA (1) | 2024.01.22 |
| [강의노트] 통계 - 검정통계량, t-value (1) | 2024.01.19 |



