스파르타코딩클럽의 강의와 Kmooc/공돌이 수학정리노트를 참고하여 작성하였습니다
1. 통계적 가설검정
목적: 주어진 자료가 특정 가설을 충분히 뒷받침하는지 여부를 결정하는 통계쩍 추론 방법
2. 검정가설의 절차
귀무가설 검증과정
귀무가설 가정 -> 실험 수행 -> 귀무가설로는 결과 해석 불가 -> 귀무가설 기각 -> 대립가설 채택
귀무가설: 현 상태에 대한 잠정적 가정(새로울 게 없다 -> 목적: 기각하고 싶음)
대립가설: 우리가 알고 싶은 것(새로운 것이 있다)
- 귀무가설이 참이라면 이런 극단적인 값을 가지는 통계량을 구하기 힘들다 -> 귀무가설 기각
- 1) 귀무가설을 기각한다(대립가설이 참이기 때문에 귀무가설이 참이라고 할 수 없다)
- 2) 대립가설이 참이라고 말할 충분한 증거가 없다(귀무가설을 기각할 수 없다)
- 귀무가설이 틀렸다는것을 증명하기 어려우니 (귀무가설이 맞다고 가정하고) 대립가설을 통해 이러한 대립가설의 증거가 있으니, 귀무가설이 맞을리가 없다(기각한다)
💡예시
Before: 인스타카트를 이용하는 유저들은 주말에 조금 더 많은 수량의 상품을 구매할 것이다
After
귀무가설: 인스타카트를 이용하는 유저들의 1회 상품 구매량은, 주중과 주말에 차이가 없다
대립가설: 인스타카트를 이용하는 유저들의 1회 상품 구매량은, 주중과 주말에 차이가 있다
-> 귀무가설을 반박할 증거가 충분한지/아닌지 아는 것이 목적
*귀무가설을 이용한 검증방식은 "무죄추정의 원칙"과 유사함. 무죄추정의 원칙을 따르면 용의자나 피고인은 유죄로 판결확정(귀무가설이 기각)되기 전까지 무죄로 추정한다(즉, 귀무가설이 기각되지 않은 상태가 원칙이다)
**이때, 유죄로 판결하기 위해선 피고인이 실제로 무죄라고 가정했을 때 발생할 수 없는 증거나 상황(통계적으로 유의미한 수준)이 뒷받침 되어야 함 -> 귀무가설을 기각하기 위해서 귀무가설이 참이라고 가정하기엔 발생할 수 없는 증거(대립가설의 증거)가 뒷받침되어야 함
*** 그러나 귀무가설을 기각할 수 있다고 해서 대립가설을 증명하는 것이 아니다! 귀무가설의 검증 과정은 "검증실패"에 주안점을 두는 것
https://angeloyeo.github.io/2020/03/25/hypothesis.html
2) 검정통계량(t-test,anova등): 법정시스템에서 증가와 같은 역할, 검정통계량의 값이 극단적이라면 귀무가설이 참인지 여부에 의문을 표시하게 된다 -> 귀무가설 기각 가능
- (관측치- 귀무가설하에서 기댓값)/표준편차
- [(관측치- 귀무가설하에서 기댓값]^2)/표준편차
3)검정통계량의 표본분포: 귀무가설이 참이라는 가정하에 검정통계량의 분포로 이를 통해서 검정통계량의 값이 극단인지의 여부를 판별가능 ->. 검정통계량의 분포가 극단적이면 귀무가설이 참이라는 가정이 잘못됨 = > 검정통계량의 분포가 극단적이면 귀무가설 기각
귀무가설하에서 이런 검정통계량의 분포는 표준정규분포, 카이제곱분포,T-분포를 따르며 카이제곱분포와 T-분포의 경우<자유도>라는 모수를 가짐
3. 가설의 검정 TEST
(1)가설을 검정할 수 있는 통계량 생성

(2) 통계량이 따르는 분포 확인

(3) 검정을 위한 하나의 검정통계량(Test Statistic) 생성

4. P-value와 귀무가설
검정통계량(t-value)에 관한 확률
즉, *귀무가설이 참이라는 전제하에 우리가 얻은 검정통계량보다 크거나 같은 값을 얻을 수 있는 확률
*두 표본 평균의 차이를 검증한다고 할 때, 두 표본집단의 모집다는 같을 것이라는 가정을 전제
-> 우리가 얻은 데이터에 있는 두 표본 집단이 같은 모집단에서 나온거라고 생각할 때
우리가 이런 검정통계량(t-value)을 얻었는데 이거 얼마나 말이 되는 확률(p-value)이지?
- 의마: 귀무가설이 참이라는 전제하에 우리가 관측한 검정통계량(예,t-value)의 값이나 혹은 그보다 더 극단적인 값을 얻을 확률, 귀무가설이 정확하다는 가정하에서 실게 관찰된 결과만큼 극단적인 검정 결과를 얻을 확률
-> p-value가 주어진 기준값(유의수준)보다 작다면 검정통계량의 값이 극단적
-> p-value가 주어진 기준값(유의수준)보다 작다면 귀무가설 기각
*단측검정을 쓰는 것은 반드시 과학적 근거가 있거나 선행연구 결과에서 이런 방향으로 있을 수 없다 등의 근거가 있을 때만 가능
양측검정/단측검정인지 여부에 따라 검정통계량의 분포를 이용하여 P-value를 계산한다
P-value가 주어진 유의수준(보통 0.05)보다 작은 경우 귀무가설하에서 이러한 결과를 얻을 가능성이 극단적(5%이하)라고 생각하고 귀무가설을 기각한다(같은 모집단이 아니다)
P-value를 구하기 위해서 귀무가설하에서 검정통계량의 분포를 알아야 하는데, 이 분포를 카이제곱분포라고 한다
**카이제곱분포
일반적으로 p-value가 연구를 시작할 때 세운 기준 수치보다 작으면 귀무가설이 틀렸다고 생각
➡️ 이러한 기준 수치를 신뢰 수준 Confidence Level이라고 함
4. 95% 신뢰구간의 의미
- 모집단에서 표본을 추출하는 수많은 경우의 수가 있는데 이러한 경우의 수의 평균을 모으면 정규분포를 이룬다
- 즉, 추출한 표본의 평균은 모평균으로 부터 2*표준오차(sem)범위 안에 95% 확률로 들어온다
-> 표본추출은 무수하게 많은 조합으로 추출할 수 있으며 100번정도 반복 샘플링을 해 보았을 때 95번 정도는 2*표준오차 안에 모평균이 들어있다

- 대학생의 평균 연애횟수가 2.7에서 3.7사이에 있을 때 확률이 95%이다(X)
- 대학생을 대상으로 표본을 100개뽑아 연애횟수에 대한 신뢰구간을 만든다면 이중 평균적으로 95개의신뢰구간이 모집단의 평균 연애횟수를 포함하고 (2.7,3.7)은 이렇게 구해진 100개의 신뢰구간 중 하나다(O)-> 100개의 표본을 이용하여 만든 신뢰구간에서 빨간색으로 표시된 1개의 신뢰구간은 실제 모집단의 평균 연애횟를 포함하지 않는다(표본의 크기는 달라도 됨)
- 신뢰수준이 95%이고 표본오차가 +-3%(2xSEM=3%)인 여론조사에서 A후보40%, B후보 36%의 지지율을 보일 경우
- -> 신뢰수준 95%, 표본오차 +-3%에 따르면 A후보 지지율의 모비율은 37~43%사이에 존재할 확률이 95%이고, B후보 지지율의 모비율이 33~39%사이에 존재할 비율이 95%이다
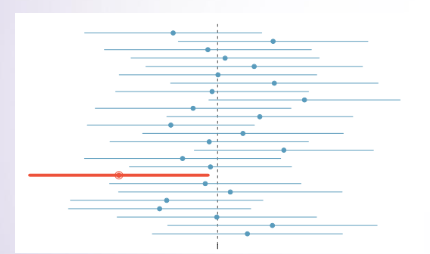
https://angeloyeo.github.io/2021/01/05/confidence_interval.html
신뢰 구간의 의미 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
4. 신뢰수준과 오류
- 통계적 가설검정의 오류: 1종오류, 2종오류
- 1종오류: 귀무가설이 맞았는데 기각하는 것
- 1종오류가 발생하지 않을 가능성: 신뢰수준
- 1종오류가 발생할 가능성: 유의수준
- 2종오류: 귀무가설이 틀렸는데 기각하지 못하는 것
5. t-test의 한계
- t-test는 보통 두 집단을 대상으로 함
- 3개 이상의 집단을 대상으로 평균을 검정하기에는 부족
예를 들어 A, B, C에 대한 평균을 비교할 때
세 쌍:(A, B), (B, C), (A, C)에 대해 3번 검정을 진행할 수 있지만 회차를 반복하며 신뢰 수준이 떨어짐
해결책: anova
'학습노트 > 통계' 카테고리의 다른 글
| [통계학습] 데이터와 표본분포(2) (0) | 2024.05.14 |
|---|---|
| [학습노트] 통계2. 데이터와 표본분포 (1) (0) | 2024.04.01 |
| [학습노트] 통계1. 탐색적 데이터 분석 (0) | 2024.04.01 |
| [강의노트] 통계 - 검정통계량, ANOVA (1) | 2024.01.22 |
| [강의노트] 통계 - 검정통계량, t-value (1) | 2024.01.19 |



