
5.5 분균형 데이터 다루기
- 불균형 데이터에서 예측 모델링 성능을 향상시킬 수 있는 방법
- 과소표본 : 분류모델에서 개수가 많은 클래스 데이터 중 일부 소수만을 사용하는 것 (유의어 : 다운샘플)
- 과잉표본 : 분류모겔에서 희귀 클래스 데이터를 중복하여, 필요하면 부트스트랩해서 사용하는 것(유의어 : 업샘플)
- 상향 , 하양 가중치 : 모델에서 희귀 혹은 다수 클래스에 높은/낮은 가치를 주는 것
- 데이터 생성: 부트스트랩과 비슷하게 다시 샘플링한 레코드를 빼고 원래 원본과 살짝 다르게 데이터를 생성하는 것
- z점수 : 표준화 결과
- K : 최근접 이웃 알고리즘에서 이웃들의 개수
주요개념
- 데이터의 심각한 불균형( 즉, 관심있는 결과의 데이터가 희박할 때)은 분류 알고리즘에서 문제가 될 수 있다
- 불균형 데이터를 다루는 한가지 방법은 다수의 데이터를 다운샘플링하거나 의귀한 데이터를 업샘플링해 학습 데이터의 균형을 맞추는 것이다
- 갖고 있는 1의 데이터를 모두 사용해도 그 개수가 너무 적을 때는, 희귀한 데이터에 대해 부트스트랩 방식을 사용하거나 지곤의 데이터와 유사한 합성 데이터를 만들기 위해 SMOTE를 사용한다
- 데이터에 불슌형이 존재할 경우 보통은 어느한쪽을 정확히 분류하는 것에 더 높은 점수를 주게 되어있고, 이러한 가지 비율이 평가 지표에 반영되어야 한다
6.1 최근접이웃
- 이웃 : 예측변수에서 값들이 유사한 레코드
- 거리 지표 : 각 레코드 사이가 얼마나 멀리 떨러져 있는지를 나타내는 단일 값
- 표준화 : 평균을 뺀 후에 표준편차로 나누는 일
- z점수 : 표준화를 통해 얻은 값
- K : 최근접 이웃을 계산하는 데 사용되는 이웃의 개수
K-NN : 거리기반의 알고리즘, 어떤 새로운 데이터로부터 거리가 가까운 K개의 다른 데이터의 레이블을 참고하여 K개의 데이터 중 가장 빈도 수가 높게 나온 데이터의 레이블로 분류하는 알고리즘
> 유사한 데이터들의 평균을 예측값으로 사용하여 회귀 알고리즘으로 사용 가능하다
| 장점 | 단점 |
| - 분류 및 회귀로 사용 가능 - 사용이 간단하여 학습이 빠름 - 별도의 학습 불필요 - 범주로 분류할 기준이 없어도 사용 가능 |
- K값의 결정이 어려움 - 연속형 데이터가 아닐 경우 유사도 정의가 어려움 - 이상값 존재시 성능저하 발생 |
- K값은 학습의 난이도와 데이터의 개수에 따라 결정될 수 있음 > 일반적으로 훈련개수의 제곱근으로 설정
- K값이 너무 크면 주변의 데이터와 떨어져 분류가 잘 이루어 지지 않음 > 과소적합
- K값이 너무 작으면 데이터 하나하나에 민감 > 과대 적합
<알고리즘 절차>
- 사전 모델링 없이 훈련 데이터 저장 = lazy model
- 초기 K값 정의(새로운 데이터 분류에 참여할 이웃 데이터 수)
- 새로운 데이터 각 데이터의 거리 계산(유클리드 거리, 마할라노비스거리 등)
- 가장 가까운 K개의 데이터 선정
- 새로운 데이터를 선정된 K개의 데이터 중 가장 많은 집단으로 분류(majirity Voting)
<유클리드 거리 = L2 Distance>
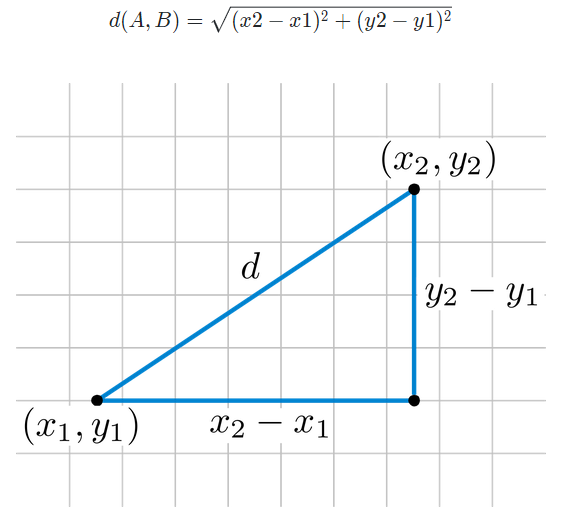
<맨하튼 거리 = L1 Distance>
유클리드 공식처럼 직선으로 이동할 수 없는 건물들이 많은 체계적인 지역의 거리를 재기 위한 공식
대각선의 거리를 고려하지 않는다
즉, 맨하튼 거리는 항상 유클리드 거리보다 같거나 크다
d(P1,P2 ) = ∣p1−p2∣+∣q1−q2∣
검은색 점(P1, P2)의 거리
초록색 : 유클리드 거리
맨하튼 거리 : 빨간색, 파란색, 노란색(모두 거리가 같다)

범수값 범위의 조정 : 정규화
K-NN 알고리즘은 데이터 포인트들 간의 거리를 계산하여 가장 가까운 이웃을 찾습는다.
> 데이터의 각 특징(feature)들이 서로 다른 범위를 가진다면, 큰 범위를 가진 특징이 거리 계산에 더 큰 영향을 미치게 된다
예시 : 월급(1~100,000,000)과 키(1~200)의 거리계산
> 월급으로 대다수의 계산이 이루어짐

정규화를 하지않을 경우
Distance(A,B)= √ (160−170)^2+(40,000,000−100,000,000)^2 = 60,000,000
Distance(A,C)= √
> 급여로만 계산이 이루어지고 각 키에 대한 차이는 무시된다
정규화의 종류
1. 최대 -최소 정규화 : 0 ~ 1사이의 값이 나옴
> 데이터가 특정 분위내에 있을때 유용, 각 특징의 분포가 서로 다를 때 적합 + 이상치에 민감

2. Z-점수 정규화 : 평균이 0, 표준편차가 1인 분포로 변환
> 데이터가 정규 본포를 따를 때 효과적, 이상치에 덜 민감 > 좀더 로버스트 함~
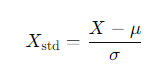
이상치에 덜 민감한 이유 : 이상치가 반영된 표준편차로 나누기 때문
(이상치가 커지면 표준편차도 커지기 때문)
정규화 거리를 통한 계산(Min-Max)
키 150 ~200
급여 120,000,000 ~ 30,000,000

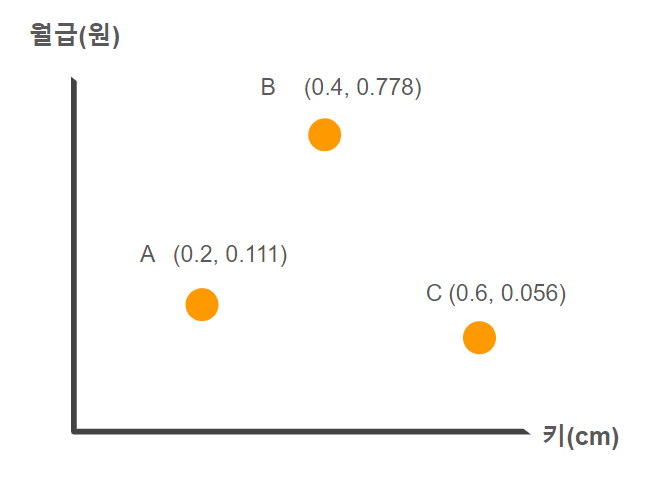
Distance(A,B) = √ (0.2−0.4)^2+(0.111−0.778)^2 = 0.696
Distance(A,C) = √ (0.2−0.6)^2+(0.111−0.056)^2 = 0.404
Distance(B,C) = √ (0.4−0.6)^2+(0.778−0.056)^2 = 0.749

bias 편향 - variance분산의 trade off
모델링 결과에 대한 오차에는 편향과 분산이 있음
예) 예측 결과
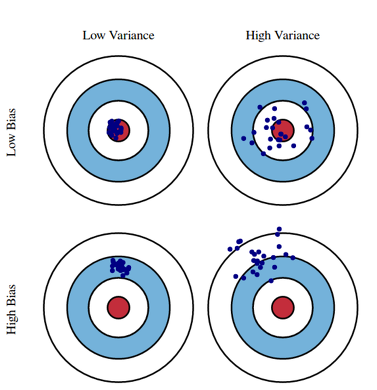
편향 : 학습 알고리즘에서 잘못된 가정을 했을때 발생하는 오차
편향 오차가 높다는 것(high bias)은 실측치와 예측치간의 오차가 크게 벌어진 상황
> 과소적합의 경향 : 모델이 단순 (예: 선형회귀)
분산 : 트레이닝 데이터의 변동으로 인해 발생하는 오차
분산오차가 높다는 것(high variance)은 노이즈까지 학습하여 예측범위가 넓은 상황
> 과대적합의 경향 : 모델이 복잡(예 : 고차 다항 회귀, 심층 인공신경망)
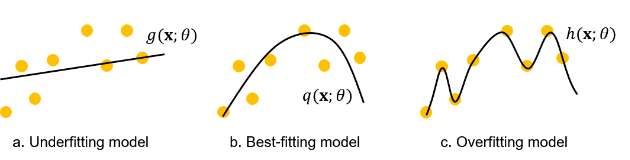
a는 너무 과소적합하고 c는 너무 과대적합하다
b와 같이 편향과 분산이 적절하게 최소화된 예측모델을 만들어야 하는데
평향과 분산을 동시에 최소화 할 수 없다
주요개념
- K-최근접이웃방법이란 유사한 레코드들이 속한 클래스로 레코드를 분류하는 방법
- 유사성(거리)은 유클리드 거리나 다른 관련 지표들을 이용해 결정한다
- 가장 가까운 이웃 데이터의 개수를 의미하는 K는 학습 데이터에서 얼마나 좋은 성능을 보이는지를 가지고 결정한다
- 일반적으로 예측변수들을 표준화한다 > 이를 통해 스케일이 큰 변수들의 영향력이 너무 커지지 않도록 한다
- 예측 모델링의 첫 단계에서 종종KNN을 이용한다 > 이렇게 얻은 값을 다시 데이터에 하나의 예측변수로 추가해서 두 번째 단계의 모델링을 위해 사용한다
'학습노트 > 통계' 카테고리의 다른 글
| [통계학습] 부스팅과 주성분 분석 (0) | 2024.06.25 |
|---|---|
| [통계학습] 통계적 머신러닝(2) (0) | 2024.06.24 |
| [통계학습] 분류 (2) (0) | 2024.06.12 |
| [통계학습] 분류 (1) (1) | 2024.06.10 |
| [통계학습] 회귀와 예측(2) (2) | 2024.06.05 |



