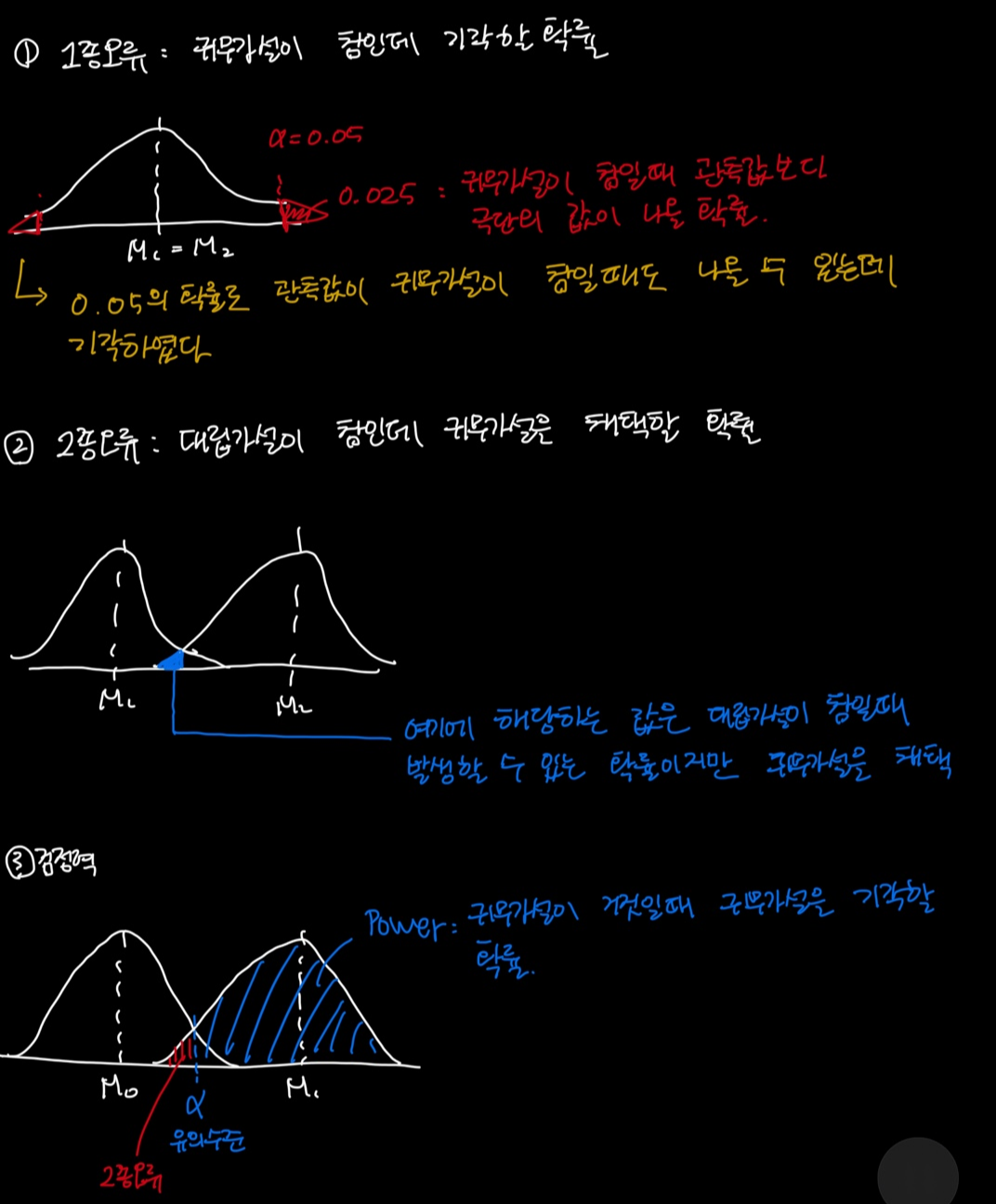
이전 복습



변이성 : 추정치가 표본에 따라 얼마나 변화하는지 알 수 있음. 많이 퍼져있을 수록 변이성이 강함
편향성 : 표본분포의 평균이 모수의 값과 동일할 때 통계량은 모수의 분편추정량
> 통계 B는 평균4아리 있기 때문에 편향적이고 모수를 과소 평가한다
신뢰도 : 어떤 방법이 장기적으로 성곡하는 비율로, 이런 형태의 구간이 관심있는 모수를 얼마나 자주 포착하는지 나타냄
90%의 신뢰도에 대한 정확한 해석
조사요원이 반복하여 분리된 독립적 표본으로부버 20개의 구간을 만든다면, 실제 비율을 얻기위한 18개의 구간을 예산할 수 있다
이 과정을 여러 번 반복한다면, 생성된 구간들의 약 90%는 후보자를 지지하는 유권자의 실제 비율을 포착가능
95%의 신뢰구간으로 (110,120)
구간 (110,120)안에 실제 모평균이 존재할 것이라고 95% 장담가능
신뢰도가 95%-> 99% 증가
신뢰도가 증가하면 신뢰구간이 더 넓어지면서 오차범위는 증가한다. 더 커진 오차범위는 관심있는 모수를 포함할 가능성이 더 큰 넓어진 신뢰구간을 형성
모표본표준편차(추정치) = 모표준편차/표본의 제곱근
확률표본평균이 표본평군 표준편차의 2배안에 있을 확률은 약 95%
신뢰구간을 추론하기위한 조건
임의성 : 자료는 임의 표본 혹은 무작위 실험으로부터 나와야 한다
일반성(정규성) : 표본분포는 정규분포를 따라야하기 때문에 적어도 성공횟수와 실패횟수는 10이상이어야 한다

독립성 : 각각의 관측값은 독립, 비복원추출을 한다면 표본의 크기는 모집단의 10%를 초과하면 안된다
독립이 되어야 표준편차의 공식을 사용할 수 있다
p에 대한 신뢰구간을 만든다면 실제p를 알지 못하므로 p의 추정치를 사용하는데 이를 표준오차라고 한다
표준오차에 대한 공식


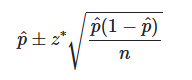

P-Value : 귀무가설이 참이라고 가정하면 표본에 대한 통계량을 얻을 확률

귀무가설과 대립가설
유의성검정은 어떤 귀무가설을 기각하는 증거의 효력을 검증하기 위해 하는 것
귀무가설: 변수 = 값
예: 시민들 중 실업자 비율이 7%,즉 실업률이 이전과 차이가 없다
대립가설은 우리가 찾고자하는 증거가 뒷받침되는 가설
대립가설 : 변수 > 값 / 변수 < 값 / 변수 != 값
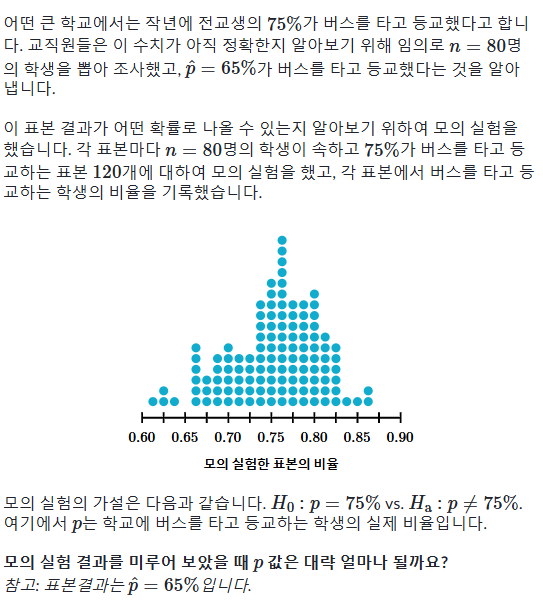

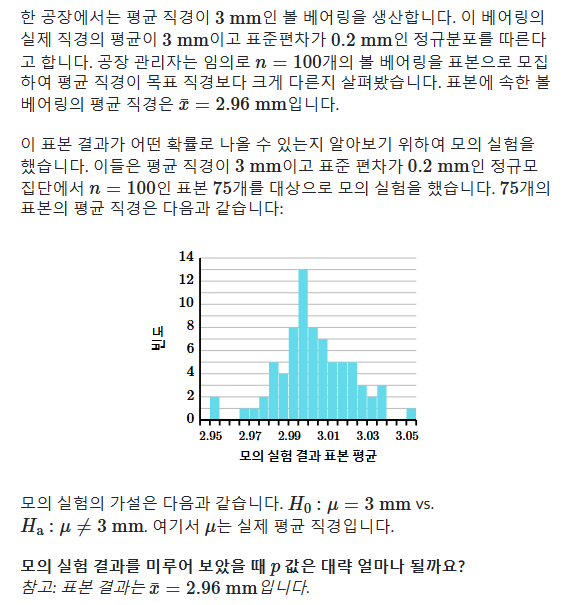
표본평균은 가설평균보다0.04mm작고, 표본75개 중 3개의 결과는 이 차이와 같거나 더 많거나 적게 차이납니다.
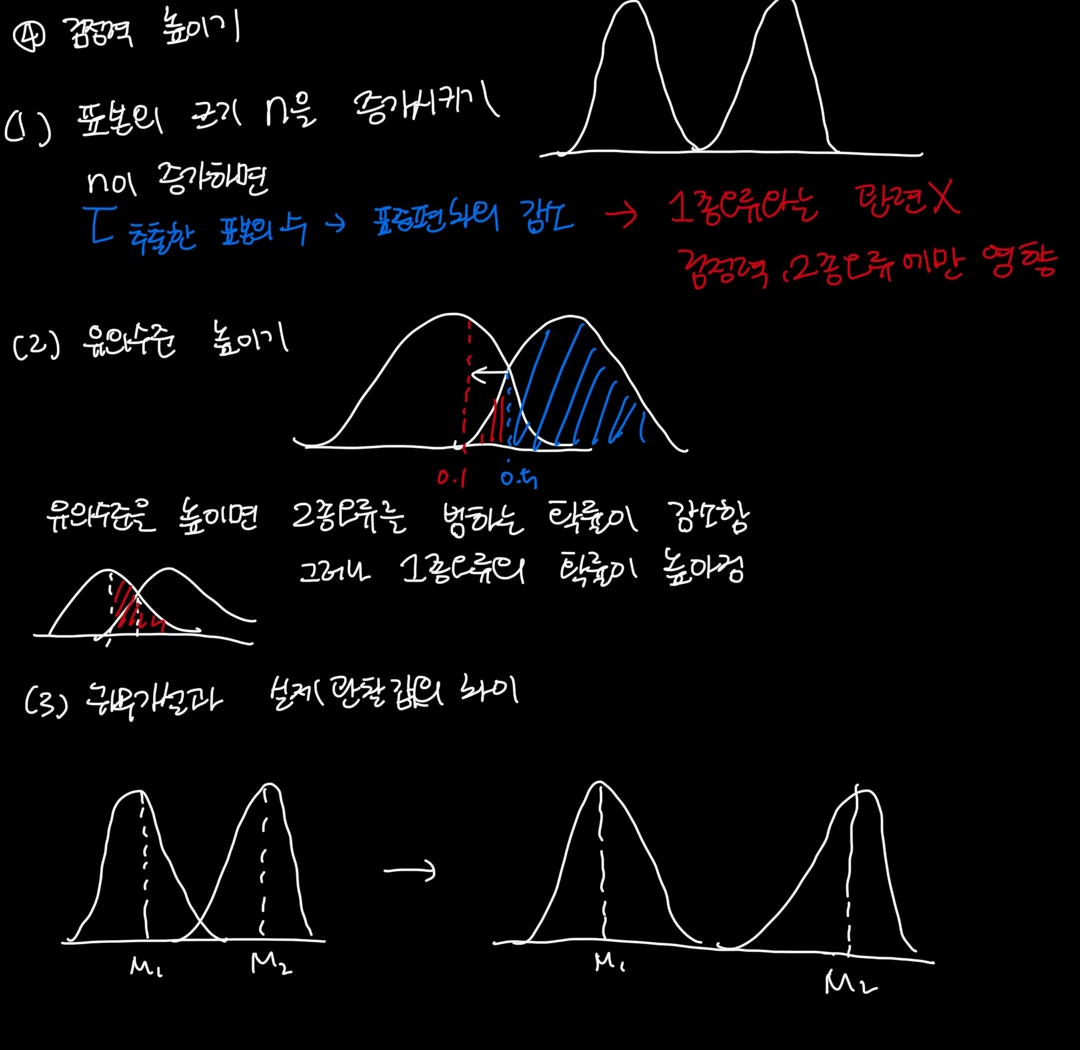
검정력 = 귀무가설이 거짓일 때 맞는 행동을 할 확률 = 귀무가설이 거짓일 때 귀무가설을 기각할 확률
= 1 - 귀무가설이 거짓인 가정하에 이를 기각하지 못하는 확률( 2종오류 )
= 2종오류가 발생하지 않을 확률
'학습노트 > 통계' 카테고리의 다른 글
| 오답노트 (0) | 2024.08.19 |
|---|---|
| [통계 학습] 칸 아카데미 오답노트6 (0) | 2024.08.12 |
| 통계 학습] 칸 아카데미 오답노트4 (0) | 2024.07.31 |
| 통계 학습] 칸 아카데미 오답노트3 (0) | 2024.07.19 |
| 통계 학습] 칸 아카데미 오답노트2 (0) | 2024.07.12 |



