7,8단원 복습

조건부확률 및 순열 계산 부족..ㅠ,ㅠ

9~10단원
< 이산변수 >
고정된 시행횟수가 있고 구해야 하는 변수는 성공횟수
< 기하변수 >
고정된 시행횟수가 없고 구해야 하는 변수는 시행한 횟수

처음 방문한 사람들에 대한 확률:
계정을생성하지않음
(0.15)(0.85)^5

- 6번째 이후 슛을 처음 성공시킬 확률 = 6번째까지 슛을 실패할 확률
- 바코드를 잘못 읽기 전까지 바코드를 10개 초과해서 읽을 확률 = 앞의 10개이 바코드를 올바르게 읽을 확률
- 전화주문 전까지 받은 주문건수가 5건 미만일 확률 = 1- 앞의 주문건수 4건이 모두 전화주문이 아닐 확률 = 앞의 4건중 1개는 전화주문이어야 함

상대도수 = 절대빈도수 / 표본공간의 크기
- 새로운 고객수가 1일때 상대도수 = 153/400 = 0.382
- 새로운 고객수가 2일때 상대도수 = 110/400 = 0.275
- 새로운 고객수가 3일때 상대도수 = 77/400 = 0.192
- 새로운 고객수가 4일때 상대도수 = 39/400 = 0.097
- 새로운 고객수가 5일때 상대도수 = 21/400 = 0.052
모든 확률변수에 대한 상대도수 X 확률변수의 합 = 2.16
따라서 5일 동안 늘어난 고객 수의 가댓값은 5 X 2.16 = 10.81

평균값 = 상대도수(장난감 개수 / 총장난감 개수) X 확률변수의 총합 = 기댓값
상대도수 = 장난감 개수 / 총장난감 개수

기댓값이 5인 것을 어디서..?

기댓값 = 모든 확률변수에 대한 대응되는 확률 X 확률변수의 총합

2일동안 수익의 기댓값
(0.49)*$100 + (0.42)*$60 + (0.09)*$20 = 76

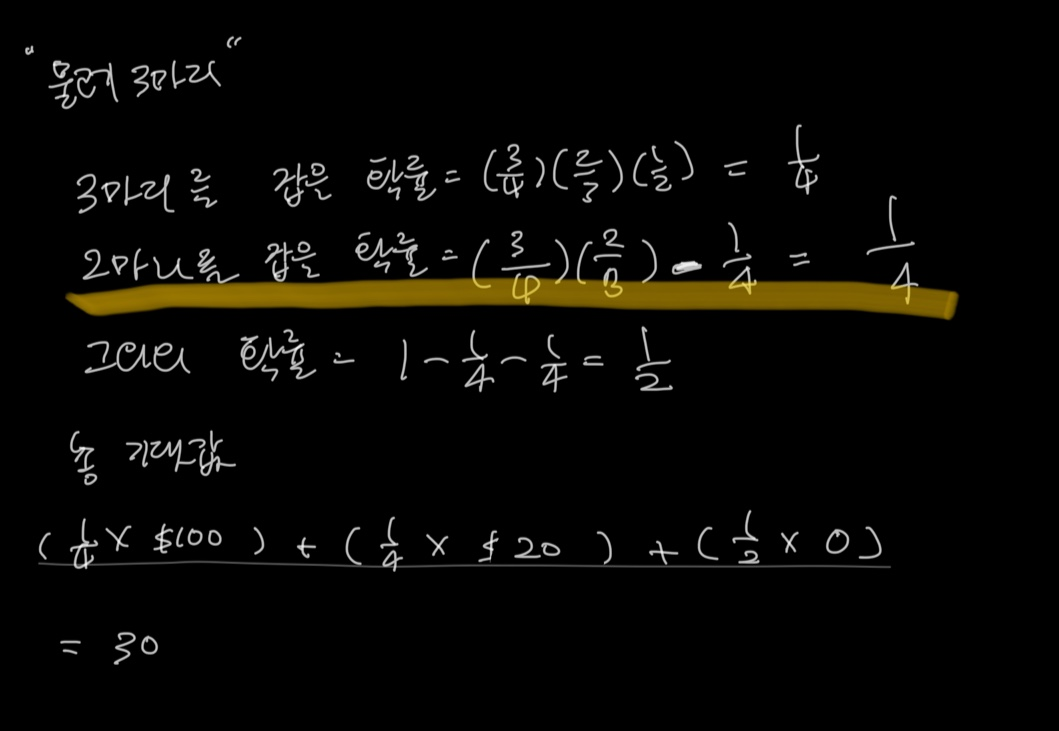
*2마리를 잡을 확률은 3마리를 잡을 확률에 포함되므로 중복값을 제외


< 표본비율의 평균과 표준편차 >
표본비율의 평균 = 표본비율의 표본분포 평균은 모비율과 동일
표본분포의 표준편차
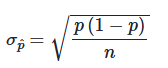

답 : 표본의 크기가 작기 때문에 모집단의 형태와 가까움(오른쪽으로 치우침)
1. 모집단이 정규분포를 따르지 않을 때
n>=30이면 표본평균은 정규분포를 따르지만
n<30이면 표본평균은 정규분포를 따르지 않음
2. 모집단이 정규 분포를 따르지 않을 때
표본평균의 표본분포 또한 크기와 상관없이 정규분포를 따름
불편Unbiased = 편의가 없다 = 편향되어 있지 않다(치우침이 없음) = 추정량의 기대값이 모수와 동일
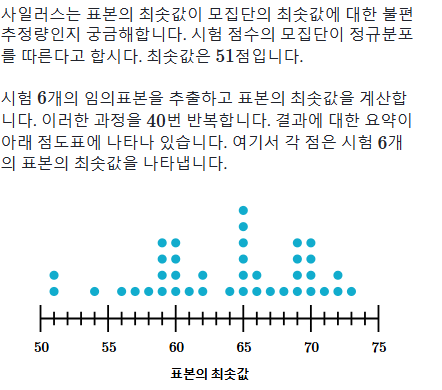
모집단 : 정규분포, 최솟값은 51
표본분포의 평균이 모수의 값과 동일할 때 통계향의 모수는 불편추정량
모집단의 최솟값이 51이고 표본의 최솟값의 중심이 51위에 있음
즉, 모집단의 최솟값을 과대평가하기 때문에 표본의 최솟값은 편향추정치
* 표본분표의 평균이 모수와 다름
'학습노트 > 통계' 카테고리의 다른 글
| [통계 학습] 칸 아카데미 오답노트6 (0) | 2024.08.12 |
|---|---|
| [통계 학습] 칸 아카데미 오답노트5 (0) | 2024.08.03 |
| 통계 학습] 칸 아카데미 오답노트3 (0) | 2024.07.19 |
| 통계 학습] 칸 아카데미 오답노트2 (0) | 2024.07.12 |
| [통계 학습] 칸 아카데미 오답노트1 (0) | 2024.07.08 |



