
1. Z-score
1) z-score :평균으로부터 표준편차의 몇배만큼 떨어져 있는지를 나타낸다
Z = ( 자료값 - 평균 ) / 표준편차
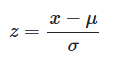
2) z-score의 특징
- 양의 z점수는 측정값이 평균보다 높다
- 음의 z점수는 측정값이 평균보다 낮다
- 0에 가까운z점수는 측정값이 평균과 비슷하다
- z값이 3또는 -3을 벗어나면 흔하지 않은 값임을 의마한다
- 표준편차의 3배 만큼 떨어진 수
3) 정규분포의 특징
- 대칭인 종 모양
- 평균과 중앙값은 같고 중앙에 위치
- 자료의 약 68%는 평균으로부터 표준편차의 1배 내에 위치
- 자료의 약 95%는 평균으로부터 표준편차의 2배 내에 위치
- 자료의 약 99.7%는 평균으로부터 표준편차의 3배 내에 위치ㅊ
4) 표준정규분포표 : 주어진 z-score보다 낮은 값들의 비율

< 문제 >

방법
1) 표준 정규분포표에 따라 z점수가 하위 70%인 점수를 찾는다 = 0.53
 |
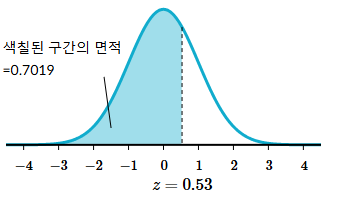 |
2) z점수가 0.53일때 원래 값은
( 값 - 80 ) / 9 = 0.53
값 = 0.53*9 + 80 = 84.77
2. 상관관계와 선형회귀
1) 산점도
: 두 변수의 관계를 보여주는 자료 표시의 방법
2) 상관계수(r)
: 두 변수의 방향과 선형 관계를 나타내는 지표
- -1과 1사이에 존재
- 강한 양의 선형관계일수록 1에 가까움
- 강한 음의 선형관계일수록 -1에 다따움
- 선형관계가 약할수록 0에 가까움
3) 선형회귀
: 산점도 내에 존재하는 자료를 따라 직선으로 그리는 과정으로 다른 측정값을 예측할 수 있는 것
3) 최소제곱법을 통한 선형회귀식 구하기
- 최소제곱법 : 관측된 값과 예측값 사이의 오차 제곱의 합을 최소화 하는 법
- 잔차 = 실제값 - 예측값
- 예측값 = mx + b
- m = (상관계수) x (y의 표준편차/x의 표준편차)
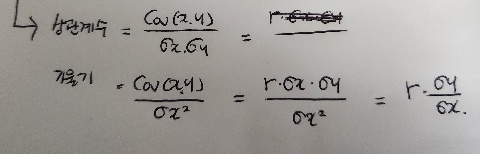
4)기울기 계산하는 원리
- 상관계수는 x와 y의 공분산을 x의 표준편차와 y의 표준편차로 나눈 값
- 선형회귀에서의 기울기는 공분산을 x의 분산으로 나눈 값
> 즉, x와 y간의 관계를 나타내는 선형회귀 모델에서 최소제곱법을 사용하여 기울기를 유도하면
공분산을 x의 분산으로 나눈 값이 된다
5) 결정계수(R^2)
: 회귀분석모델에서 종속변수의 변동을 얼마나 잘 설명하는지 나타내는 지표
R^2 = 1 - (잔차제곱의 합 / 총 제곱합)
- 잔차제곱합(분자) : 회귀모델의 오차를 나타내며, 관측값-예측값의 제곱의 총 합
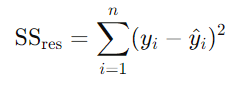
- 잔차 제곱의 합이 작으면(잔차가 작으면) 잘 예측한 것으로 결정계수는 1에 가까워진다
- 잔차 제곱의 합이 크다는 것은 예측을 잘 못한것으로 결정계수는 0에 가까워진다
- 총 제곱합(분모) : 종속변수 y의 총 변동성을 나타내며 관측값-평균값의 총 합
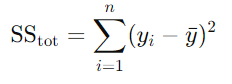
(1) 상관관계 : 두 변수가 함께 변하는 정도와 방향을 나타낸다
- 양의 상관관계, 음의 상관관계
(2) 인과관계 : 하나의 변수의 변화가 다른 변수의 변화를 직접적으로 초래하는 관계
(3) 선형관계 : 두 변수의 관계사 직선으로 나태날 수 있는 경우로 한변수가 변할때 다른 변수가 일정 비율로 변하는 것
- y = mx + c
(4) 상관계수(r) : 두 변수 간의 정도와 방향을 수치로 나타낸 지표(-1 ~ 1)
(5) 결정계수(R^2) : 회귀분석에서 독립변수가 종속변수를 얼마나 잘 설명하는지 나타내는 지표
- 0~1사이의 값으로 1에 가까울 수록 모델이 데이터를 잘 설명함
(6) 공분산 : 두 변수간의 상과 변동성을 측정하는 지표
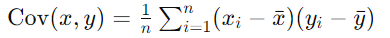
< 문제 >


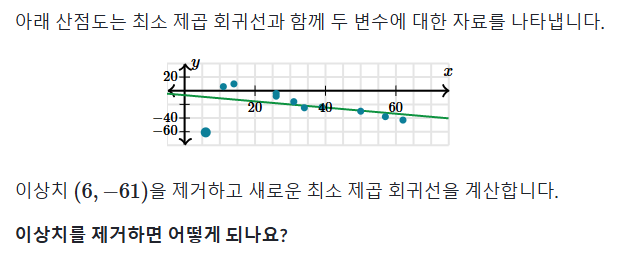
이상치를 제거하면 전체적인 잔차가 감소하고 모델의 적합성이 증가하는데
이는 관측값들이 선에 가까워지면서 관계가 강력해졌다는 것
즉, R^2이 증가한다
'학습노트 > 통계' 카테고리의 다른 글
| 통계 학습] 칸 아카데미 오답노트4 (0) | 2024.07.31 |
|---|---|
| 통계 학습] 칸 아카데미 오답노트3 (0) | 2024.07.19 |
| [통계 학습] 칸 아카데미 오답노트1 (0) | 2024.07.08 |
| [통계학습] 부스팅과 주성분 분석 (0) | 2024.06.25 |
| [통계학습] 통계적 머신러닝(2) (0) | 2024.06.24 |



