
1. 확률

- P(적어도 하루는 쿠폰을 받음) = 1 - P(6일동안 하루도 쿠폰을 받지 못함)
- 1 - 0.85^6
▶ 답 : 약 0.623
2. 조합

- (여학생만 뽑는 경우의 수) / (전체 학생을 뽑는 경우의 수)
| 여학생만 뽑는 경우의 수 : 5명중에 3명을 뽑음 | 전체 학생을 뽑는 경우의 수 : 7명중에 3명을 뽑음 |
 |
 |
▶ 답 2/7
[ 순열과 조합 ]
- 순열 : 임의로 무엇을 뽑을 때, 순서가 영향을 줌
- 조합 : 임의로 무엇을 뽑을 때, 순서에 영항을 받지 않음
3. 표본분포

- 표본분포의 평균 : 표본비율의 표본분포 평균은 모비율과 동일
▶ 답 : 표본비율의 표본평균 = 모비율 = 0.93
- 표본분포의 표준편차

▶ 답 : 0.93
[ 관련 이론 ]
- 이항분포의 : 성공확률 P를 가지는 독립시행 n번 중 성공한 횟수를 나타내는 확률분포
- 표본비율 : 전체 표본 중 성공한 비율 = 이항분포에서 성공한 횟수를 표본 크기 n으로 나눈 값
- n으로 나누는 이유 : 표본비율이 성공횟수 X를 n으로 나눈 값이기 때문
| 모집단 | 표본 비율 | 표본 비율의 분산 |
 |
 |
 |
4. 표본분포의 형태

- 평균 : 2.5
- 표분편차 1.5
- 표본의 크기 : 7
▶ 답 : 알 수 없다
[ 표본분포 추론 이론 ]
- 모집단이 정규분포를 따르지 않을 때
- n>=30이면 표본평균은 정규분포를 따르지만
- n<30이면 표본평균은 정규분포를 따르지 않음
- 모집단이 정규 분포를 따를때
- 표본평균의 표본분포 또한 크기와 상관없이 정규분포를 따름
5. 오차범위 구하기

- 오차범위 :평균(통계량)에서 (임계값)과 (통계량의 표분편차)의 곱
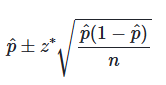
▶ 답 : 최소 23
- 1.96(z값) X 12 / √n <= 5
- 1.96 X 12 <= 5√n
- 1.96 X 12 / 5 <= √n( √n만 우변에 있도록)
- (1.96 X 12 / 5)^2 <= n
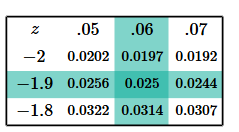
[ 신뢰구간 추론 이론1 ]
- 신뢰도가 95% = 1.96 구하기
| 신뢰구간 : 양 꼬리의 합이 5%가 되는 지점을 찾는다 | 표준정규분포표 |
 |
 |
6. 신뢰구간 구하기

| ▶ 정답 | 공식 : 통계량 +- 임계값 * 통계량의 표준편차 |
 |
 |
임의성 : SRS (단순확률표본, 임의추출)
정규성 : 다른노래일 경우의 수 30(실패의 수), 여성 노래의 경우의 수 20(성공의 수)
독립성 : 500개중 10% 이하
[ 신뢰구간 추론 이론2 ]
- 정규성 : 표본분포는 정규분포를 따라야하기 때문에 적어도 성공횟수와 실패횟수는 10이상이어야 한다
- 임의성 : 자료는 임의 표본 혹은 무작위 실험으로부터 나와야 한다
- 독립성 : 각각의 관측값은 독립, 비복원추출을 한다면 표본의 크기는 모집단의 10%를 초과하면 안된다
7. 카이제곱 검정
[통계학습] 데이터와 표본분포(3) (tistory.com)
 |
 |
'학습노트 > 통계' 카테고리의 다른 글
| [통계학습] 3장 인과추론 소개 (0) | 2024.09.18 |
|---|---|
| [통계학습] 1장 인과추론 소개 (0) | 2024.09.02 |
| [통계 학습] 칸 아카데미 오답노트6 (0) | 2024.08.12 |
| [통계 학습] 칸 아카데미 오답노트5 (0) | 2024.08.03 |
| 통계 학습] 칸 아카데미 오답노트4 (0) | 2024.07.31 |


