1. 벡터
1) 개념
벡터란 공간상에서 특정 방향과 길이를 가진 화살표이며 데이터를 시각화 하는 것을 목적으로 한다
2) 계산(벡터의 덧셈)
*음수 방향의 벡터는 나중에 벡터를 결합할 때 더하지 말고 빼야 한다
[3,2]+ [2,-1] = [5,1]
▶ 두 벡터를 더하려면 차례로 연결하고 마지막 벡터의 끝으로 이동하여 끝나는 지점이 두 벡터를 합한 새로운 벡터
▶ 교환법칙이 성립하기 때문에 무엇을 먼저 더하는 지는 중요하지 않음
3) 스케일링
벡터의 길이를 늘이거나 줄이는 것으로 스칼라(scalar)라고 하는 하나의 값을 곱하거나 스케일링해서 벡터를 늘이거나 줄인다
2[1,2] = [2,4]
▶ 벡터의 크기를 조정해도 벡터의 방향은 변하지 않고 크기만 변함
▶ 예외) 벡터에 음수를 곱하면 벡터의 뱡향이 바뀐다
4) 스팬과 선형종속
벡터를 더하고 크기를 조정하는 것으로 원하는 결과를 얻을 수 있다
벡터 V+ 벡터W의 계산으로 어떤 벡터든지 만들 수 있음
이처럼 가능한 벡터의 전체 공간을 스팬(span)이라고 함
▶ 서로 방향이 다른 벡터 두 개가 있을 때, 두 벡터는 선형독립이며 스팬은 무한하다
▶ 예외) 두 벡터가 같은 방향으로 존재하거나 같은 선상에 있으면 스팬이 제한되어 선형종속이 된다 (문제를 풀기 어려움)
2. 선형 변환
1) 기저벡터
기저벡터 : 다른 벡터의 변환을 설명하는 데 사용되는 벡더(일반적으로 길이가 1 이고 서로 수직인 양 뱡향의 벡터)
원하는 벡터 a는 기처벡터i와 j로 구성됨
▶ i = [1,0], j = [0,1]
▶ [3,2] = 3i X 2j
3. 행렬 곱셉 벡터
행렬은 2차원 이상의 숫자격자로 표현한 벡터의 집합으로 기저벡터를 적용해 다른 벡터를 변환하는 것을 행렬 벡터 곱셉이라고 함
▶ M X N 행렬 A와 r X s행렬 B가 있을때 두 행렬을 곱하기 위해서는 N과 r이 같아야 곱할 수 있다
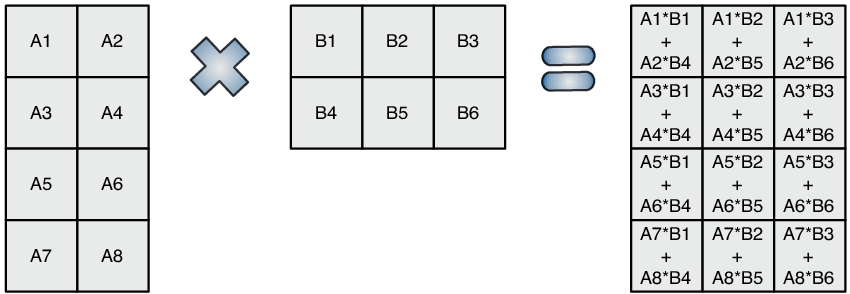
수식 확인 : https://bite-sized-learning.tistory.com/385
[이산수학]행렬의 연산(덧셈, 뺄셈, 스칼라(실수) 곱,곱셈)_예제포함
이산수학 행렬의 연산(덧셈, 뺄셈, 스칼라(실수) 곱, 곱셈) 예제포함 행렬에서 직접적으로 가능한 연산은 덧셈, 뺄셈, 스칼라(실수) 곱, 곱셈입니다. ■ 행렬의 덧셈과 뺄셈 두 행렬 A, B에서 같은
bite-sized-learning.tistory.com
4. 행렬식
두 벡터로 형성된 영역이 선형변화에 따라 크기가 얼마나 변화하는지 설명하는 비율
▶ 단준한 전단이나 화전은 면적이 변하지 않아 행렬식에 영향을 주지 않음
▶스케일링은 영역을 늘리거나 줄이므로 행렬식에 영향을 줌
▶ 방향을 뒤집으면(i와 j를 시계방향으로 위치를 교환) 스케일링 뿐만 아니라 벡터 공간의 방향도 변환이 됨
▶ 0행렬식을 테스트 하는 것은 변환에 선형 족속이 있는지 확인하는 과정
5. 특수행렬
정방행렬 : 행과 열의 수가 동일, 주로 선형 변환을 표현하는 데 사용되며 고윳값 분해와 같은 많은 연산에 필수적인 행렬
항등행렬 : 대각선의 값이 1이고 다른 값은 0인 정방행렬
역행렬 : 다른 행렬의 변환을 취소하는 행렬로 역행렬과 행렬을 곱하면 항등행렬이 됨
대각 행렬 : 항등행렬과 비슷하게 대각선에는 0이 아닌 값이 있고 나머지 값은 0인 행렬
삼각 행렬 : 대각선 행렬과 비슷한 삼각행렬은 대각선과 대각선 위쪽 또는 아래쪽에 원소가 있고 나머지 원소응 0인 행렬
희소 행렬 : 대부분이 0이고 0이 아닌 원소가 적은 행렬
6. 연립방정식과 역행렬
PASS~
7. 고유백터와 고윳값
행렬분해는 인수분해와 마찬가지로 행렬을 기본 구성 요소로 분해하는 것
▶ 다양한 머신러닝 작업에서 행렬을 다루기 쉬운 구성요소로 분할하는 데 고윳값을 사용함
'학습노트 > 통계' 카테고리의 다른 글
| [통계학습] 5장 성향점수 (0) | 2024.10.07 |
|---|---|
| [통계학습] 3장 인과추론 소개 (0) | 2024.09.18 |
| [통계학습] 1장 인과추론 소개 (0) | 2024.09.02 |
| 오답노트 (0) | 2024.08.19 |
| [통계 학습] 칸 아카데미 오답노트6 (0) | 2024.08.12 |

