스파르타 코딩클럽 과제
목적
A/B테스트를 통해 웹사이트의 랜딩 페이지 UI 실험에 따른 효과를 비교한다
- 실험 진행 기간: 약 1달간(2017/1/2 - 1/24)
- 실험 대상: 총 약 29만명 랜딩 페이지 유입 유저 → 실험군(약 14만명), 대조군(약 14만명)
- 실험 목표: 유저의 랜딩 페이지 전환율 상승
- 성공 지표(실험이 성공했다고 판단할 수 있는 지표): conversion rate(%)
- 실험 검증 방법: t-test
사용데이터
https://www.kaggle.com/datasets/zhangluyuan/ab-testing
t-test 방법
1. 가설설정
- 귀무가설(H0): 두 집단의 전환율 평균에 차이가 없을 것이다
- 대립가설(H1): 두 집단의 전환율 평균에 차이가 있을 것이다
2. 유의수준 설정 : 0.05
3. T-test실행 stats.ttest_ind
- 독립된 두 집단(new page를 본 그룹과 old page를 본 그룹)이므로 독립표본 T검정을 수행
- 두 집단의 같고 다름을 알고하 하므로 양측 검정 실행
1. 단일표본 T 검정 : stats.ttest_1samp
하나의 표본 데이터와 기준값(또는 평균)을 비교하여 통계적으로 유의미한 차이가 있는지를 검정
예시1 : 평균비교, 제품의 평균 수명이 100일인지 여부를 검정
예시2: 실험전후 비교, 신약의 효과를 검증하기 위해 환자들의 약 복용 전과 후의 특정 지표를 비교
예시3: 표본과 기준값 비교, 학생들의 수학 성적이 평균 70점과 다른지를 검정
from scipy import
stats stats.ttest_1samp(검증집단, 모평균)
2. 독립표본 T 검정 : stats.ttest_1samp
두 집단이 독립이라는 가정 하에 두 평균이 통계적으로 유의미한 차이가 있는지를 검정
등분산, 정규성 검정 후 실행
예시1 : 두 개의 그룹비교, 남성과 여성의 평균 키를 비교
stats.ttest_ind(집단1, 집단2, equal_var = True)
3. 대응표본 t 검정 : stats.ttest_rel
두 집단의 데이터가 같은 경우 (각 데이터끼리 pair를 이룸) 유의미한 변화가 있는지 검정
각 비교집단의 데이터 수가 같아야 함
예시1: 전후비교, 특정 약물을 투여하기 전과 후의 환자들의 혈압을 비교
예시2:짝지어진 데이터 비교, 부부의 소득 차이를 비교
stats.ttest_rel(집단1, 집단2)
**양측/단측 검정
1. 양측(기본값): alternative='two-sided' -> 같고 다름을 비교
2. 단측: alternative='less'/'great' -> 크고작음을 비교
- 'less' : 첫 번째 샘플의 평균이 두 번째 샘플의 평균보다 작은지를 검정
- 'greater': 첫 번째 샘플의 평균이 두 번째 샘플의 평균보다 큰지를 검정
5. 정규성 검정 shpiro()
- 정규성 검정을 위한 Shapiro-Wilk 검정을 수행
- p-value가 유의수준보다 크면 데이터가 정규분포를 따른다고 판단
6. 등분산성 검정 : levene, bartlet
1) 등분산성 검정 levene, bartlet
- 두 개 이상의 집단 간에 분산이 동일한지를 확인하는 것
- p-value가 유의수준보다 크다면 등분산성 가정을 만족
- 등분산성 가정이 충족될 때는 equal_var=True로 설정하여 등분산 t-검정을 수행하고
- 등분산성 가정이 충족되지 않을 때는 equal_var=False로 설정하여 Welch's t-test를 수행합
- 예) stats.ttest_ind(a, b, equal_var = True)
2) levene()
- 집단 내 데이터의 중앙값과의 차이를 이용하여 분산의 동일성을 검정
- 정규성 가정을 따르지 않거나 이상치가 존재시 사용
3) bartlet()
- 집단 내 데이터의 분산을 사용하여 분산의 동일성을 검정 -> 분산의 비율 계산
- 정규성 가정을 따르거나 이상치가 존재하지 않을 때 사용
t-test 실행
1. 라이브러리 및 데이터 불러오기
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
data = pd.read_csv("/Users/t2023-m0017/Desktop/실습/태블로/ab_data.csv")
data.head(10)
2. 전처리 : control 그룹에는 old_page 만 treatment 그룹으로 필터링
data_check = data[((data['group'] == 'control') & (data['landing_page'] == 'old_page')) |
((data['group'] == 'treatment') & (data['landing_page'] == 'new_page'))]
data_check[data_check["group"]=='control'].count
3. 정규성 검정
#정규성 검정
from scipy.stats import shapiro
normal1 = shapiro(control_group)
normal2 = shapiro(treatment_group)
print(normal1, normal2)>>> statistic=0.37687772512435913, pvalue=0.0
P-value가 0.05보다 작으므로 정규성이 충족하지 않는다
정규성이 충족하지 않기 때문에 levene() 수행
4. 등분산성 검정
from scipy.stats import levene
print(levene(treatment_group, control_group))>>> statistic=1.7203126672199422, pvalue=0.18965383907560016
P-value가 0.05보다 크므로 등분산성을 충족한다
5. t-test검정
from scipy.stats import ttest_ind
t_stat, p_val = ttest_ind(control_group, treatment_group,equal_var = True)
print(f"t-statistic: {t_stat:.2f}")
print(f"p-value: {p_val}")>>> t-statistic: 1.31
>>> p-value: 0.18965383906859376
P-value가 0.05보다 작으므로 두 집단의 차이가 통계적으로 유의하지 않아 귀무가설을 채택한다
T-test 해석 by 뤼튼
- t-statistic의 부호
: t-statistic이 양수인 경우는 첫 번째 집단의 평균이 더 크다는 것을 의미하며, 음수인 경우는 두 번째 집단의 평균이 더 크다는 것을 의미합니다. 여기서는 t-statistic의 값만 주어졌으므로 부호만 알 수 있을 뿐, 어떤 집단의 평균이 더 큰지는 알 수 없습니다.
- > 양측검정이라서 알 수 없음
- t-statistic의 크기
: t-statistic의 절댓값이 클수록 두 집단의 평균 차이가 크다는 것을 나타냅니다. 여기서 주어진 t-statistic의 절댓값은 1.31으로, 보통의 기준에 비하면 크지 않은 값입니다.
- > 보통의 기준이 유의수준(0.05)라면 1.31은 큰편이 아닌가?
- p-value: p-value는 주어진 데이터로부터 얻은 통계량(t-statistic) 이상의 결과가 관측될 확률을 나타내며, 작을수록 더 유의미한 결과를 의미합니다. 여기서 주어진 p-value는 0.18965383906859376로, 보통의 유의수준(예: 0.05)보다 큰 값입니다. 따라서 주어진 결과에서는 통계적으로 유의미한 차이가 있다고 말하기 어렵습니다.
A/B 테스트를 위한 지표
- 그룹별 유저 비율
- 그룹별 평균 전환율
- 일별 그룹별 평균 전환율
- 그룹별 평균 전환율
- 그룹별 고유 유저 방문에 따른 캘린더
- 일별 유저 방문수
대시보드를 통해 알아보는 랜딩페이지 실험 결과
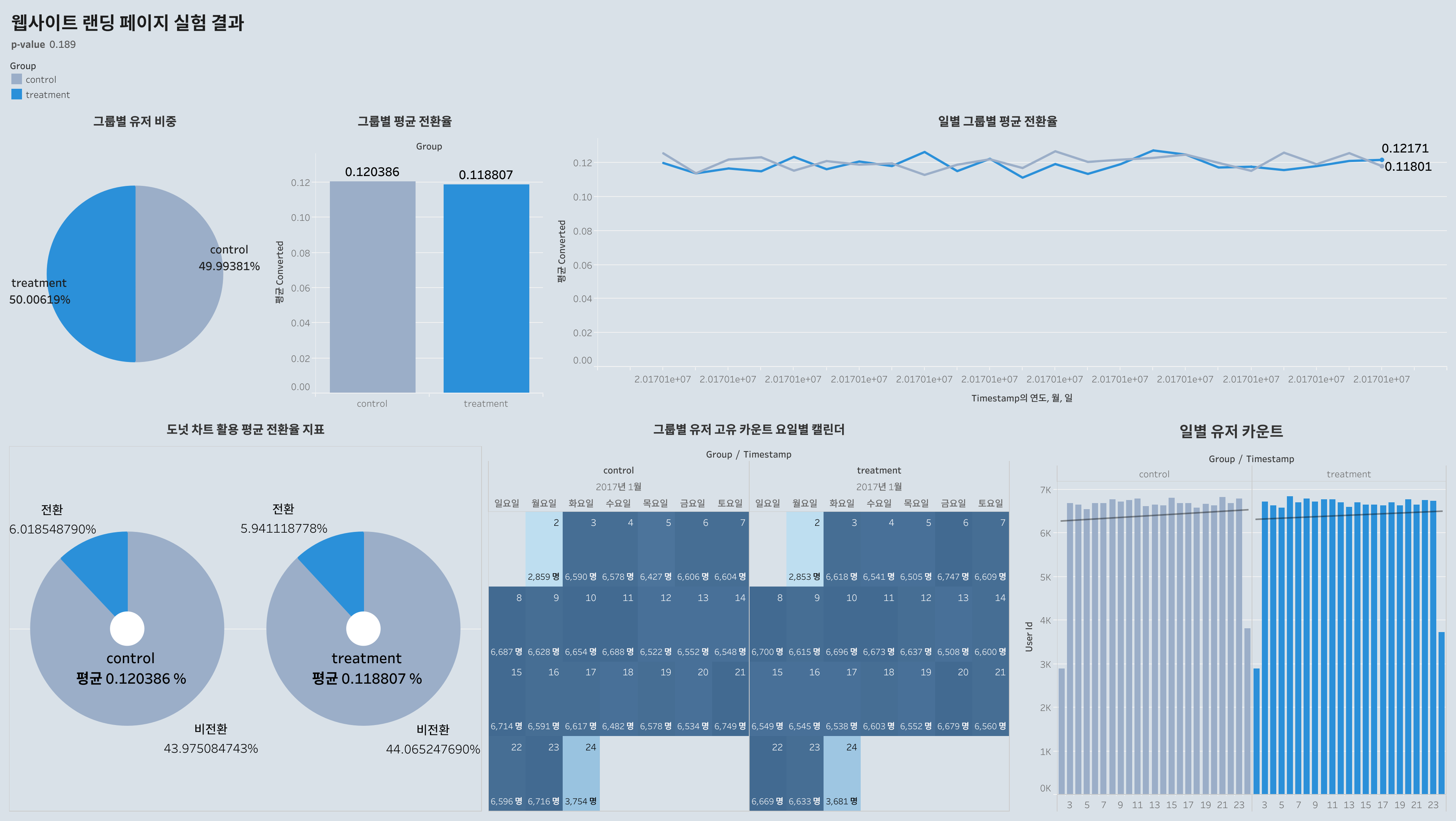
결론
두 그룹간의 차이가 없다!
'프로젝트' 카테고리의 다른 글
| 프로젝트 주제 사례 (0) | 2024.03.18 |
|---|---|
| [주식 프로젝트3] 시계열 데이터 예측하기 (0) | 2024.03.13 |
| [주식 프로젝트2] 주식데이터를 통해 기획하기 (0) | 2024.03.13 |
| [주식 프로젝트1] 야후 파이낸스 살펴보기 (1) | 2024.02.29 |
| [분석프로젝트] 히트맵, 이동평균을 통해 날씨 분석하기 (0) | 2024.02.28 |



